Lern-Archiv [2]: Mathematik
Funktionen: Potenzfunktionen [6:27]
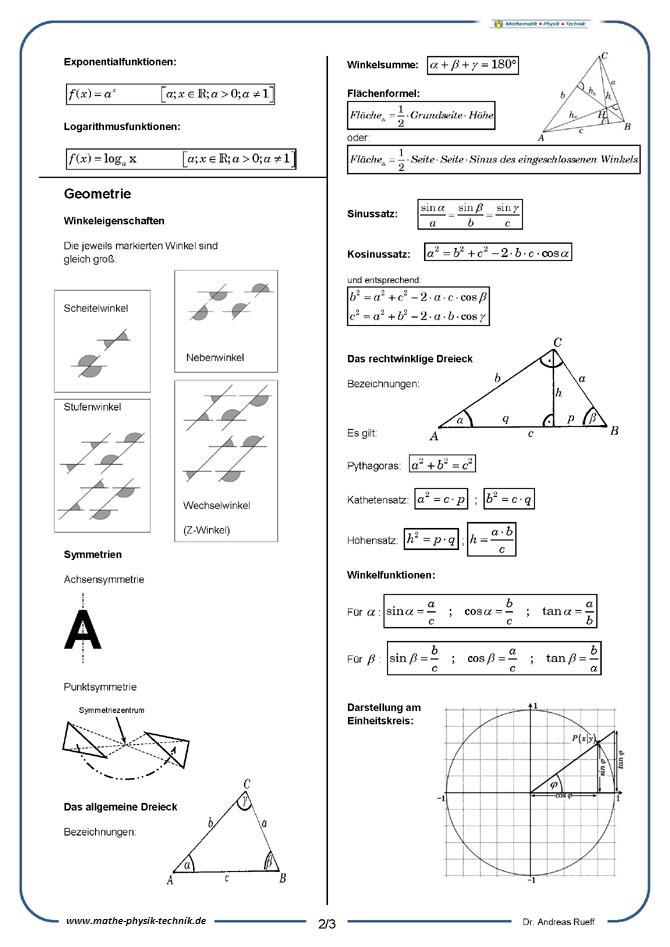
Eigenschaften von Potenzfunktionen
Die grundlegenden Eigenschaften von Potenzfunktionen werden beschrieben.
Abonnieren:
Funktionen: Exponentialfunktionen [13:17]
Eigenschaften von Exponentialfunktionen
Die grundlegenden Eigenschaften von Exponentialfunktionen werden beschrieben. Weiterhin werden zwei Anwendungsbeispiele für die Wachstumsformel und die Abnahmeformel vorgerechnet.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)
Funktionen: Wachstum und Abnahme (1): [6:34]
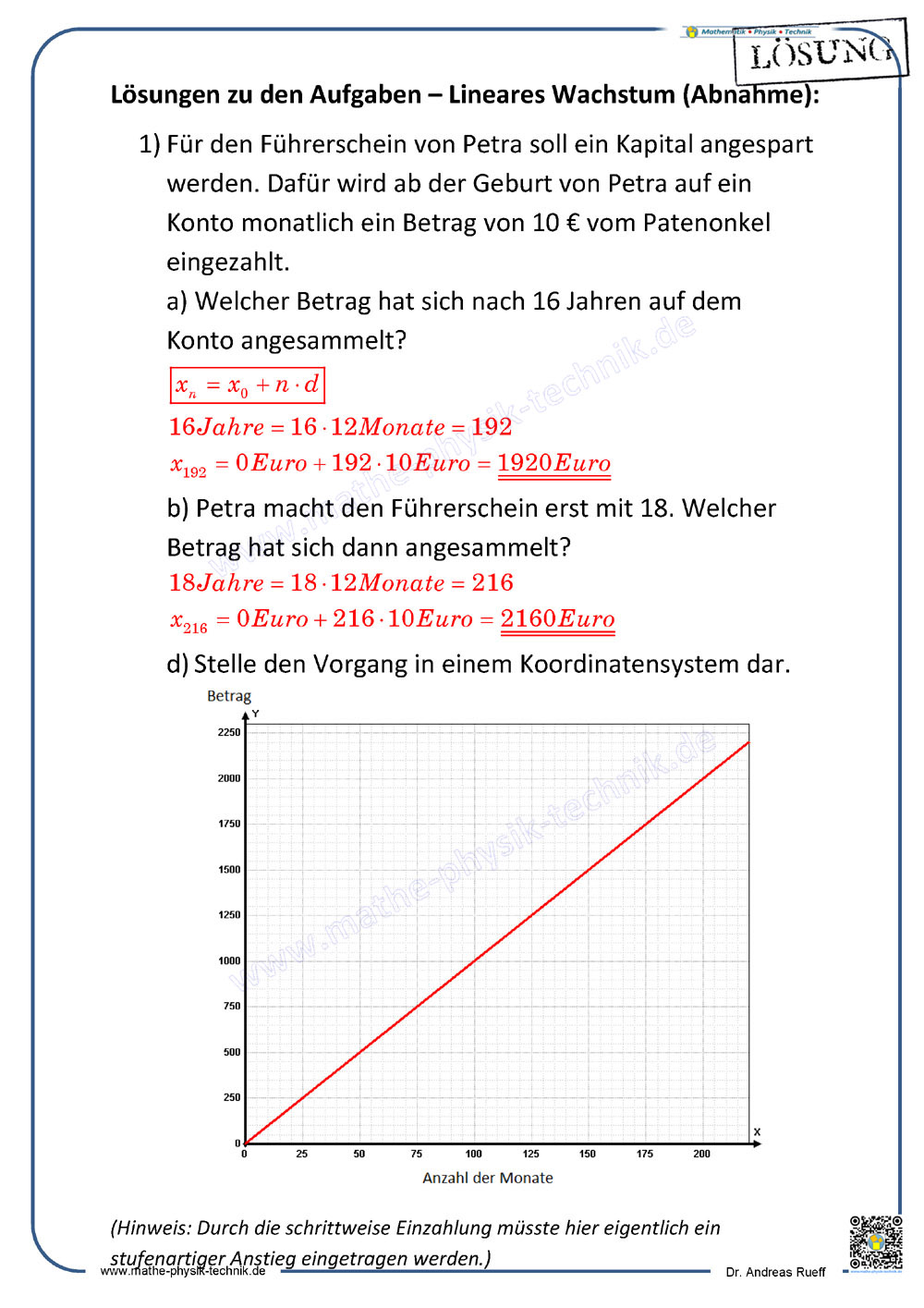
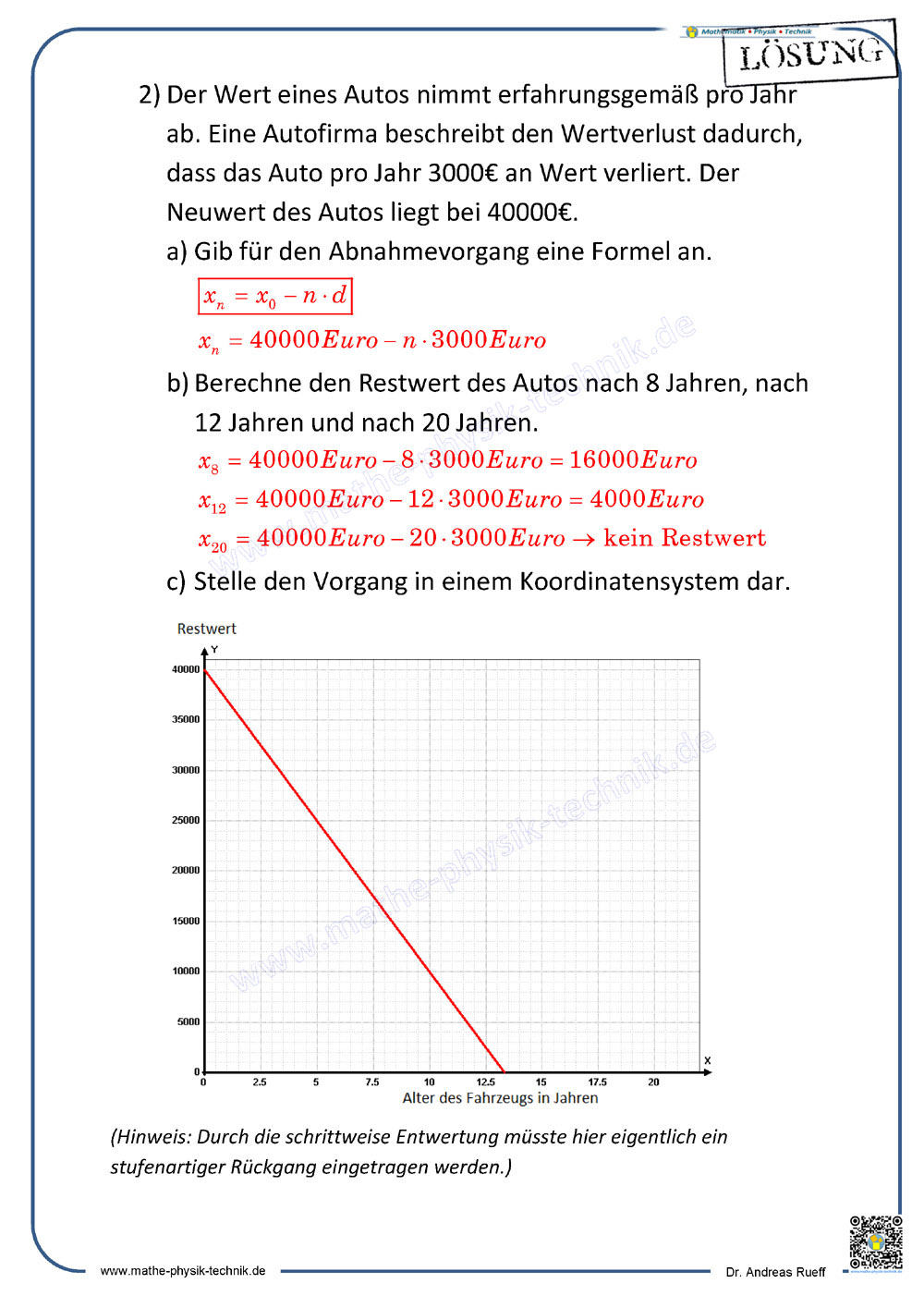
Lineare Wachstums- und Abnahmevorgänge
Im ersten Teil wird additives und subtraktives Wachstum an Beispielen erklärt. Die Wachstumsformel für lineares Wachstum und Abnahme wird hergeleitet. Die Beispiele werde dann auch grafisch dargestellt.
Funktionen: Wachstum und Abnahme (2): [8:48]
Wachstumsrate und Wachstumsfaktor
Die Begriffe Wachstumsrate (Abnahmerate) und Wachstumsfaktor (Abnahmefaktor) werden an Beispielen hergeleitet und erklärt. Abschließend wird ein Anwendungsbeispiel in schülerüblicher Schreibweise vorgeführt.
Funktionen: Wachstum und Abnahme (3): [11:34]
Exponentielle Wachstums- und Abnahmevorgänge
Im dritten Teil werden exponentielle Vorgänge, also multiplikative Zu- und Abnahme an Beispielen erklärt. Die Wachstumsformel für exponentielles Wachstum und Abnahme wird hergeleitet. Die Beispiele werde dann auch grafisch dargestellt.
Funktionen: Logarithmusfunktionen [1] [6:37]
Eigenschaften von Logarithmusfunktionen
Wie ändert sich der Funktionsgraph durch systematische Änderungen der Funktionsgleichungen?
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Funktionen: Logarithmusfunktionen [2] [2:14]
Zusammenhang zwischen Exponential- und Logarithmusfunktionen
Dargestellt wird der Zusammenhang zwischen Logarithmus- und Exponentialfunktionen durch Bildung der Umfehrfunktion.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie - Das Geodreieck: [3:20]
Grundlegende Begriffe werden am Geodreieck
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
eingeführt.
→ Übungsblatt: Geometrie Grundlagen
Geometrie - Grundlagen (1): [8:06]
Grundlegende Begriffe - Geodreieck - senkrecht - parallel
Zunächst werden einige Grundbegriffe des Geodreiecks eingeführt. Anschließend werden grundlegende Begriffe der Geometrie eingeführt (Punkt, Gerade, Strecke, Strahl). Danach wird die gegenseitige Lage von Geraden untersucht. An zwei Beispielen werden die Begriffe "parallel" und "senkrecht" verdeutlicht.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
→ Übungsblatt: Geometrie Grundlagen
Geometrie - Grundlagen (2): [3:43]
Grundlegende Begriffe - Abstand und Entfernung
An Beispielen werden die Begriffe "Abstand" und "Entfernung" von Punkten und Geraden verdeutlicht.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
→ Übungsblatt: Geometrie Grundlagen
Geometrie - Grundlagen (3): [4:14]
Grundlegende Begriffe - Koordinatensystem / Quadratgitter
An Beispielen wird die Verwendung eines Koordinatensystems gezeigt. Als einfachstes Beispiel werden im Quadratgitter Punkte und deren Koordinaten verdeutlicht.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
→ Übungsblatt: Geometrie Grundlagen
Geometrie - Flächeneinheiten: [6:14]
Flächeneinheiten und Umrechnungen
Die Umrechnung von Flächeneinheiten wird vorgeführt. Veranschaulicht wird dabei die Umrechnungszahl 100. Flächeneinheiten für große und gleine Flächeninhalte werden eingeführt.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie - Volumenberechnung (1): [5:45]
Volumenformel für den Quader /
Volumeneinheit: Kubikzentimeter
Die Berechnung des Volumens eines Quaders wird anschaulich dargestellt. Zwei verschiedene Quader werden mit Kubikzentimeterwürfeln aufgefüllt, dadurch das Volumen bestimmt und die Einheit "Kubikzentimeter" dadurch eingeführt.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie - Volumenberechnung (2): [6:20]
Volumeneinheiten und Umrechnungen
Die zur Angabe des Volumens eines Quaders notwendigen Einheiten (Kubikzentimeter, Kubikdezimeter, etc.) und deren Zusammenhänge werden anschaulich dargestellt.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Experimentelle Verfahren zur Volumenbestimmung werden in den Videobeiträgen zum Differenzenverfahren und zum Überlaufverfahren gezeigt.
Geometrie - Schrägbilder: [6:47]
Gezeigt wird die Konstruktion von Schrägbildern - Mathematik, Mittelstufe. Dabei werden die grundlegenden Regeln eingeführt und beschreiben. Anschließend werden zwei Beispiele mit allen
notwendigen Einzelheiten vorgeführt: 1) Ein Quader und 2) ein Dreiecksprisma.
Diese Darstellungsart wird auch als Kabinett-Ansicht bezeichnet.
Geometrie - Körpernetze (Abwicklungen): [3:16]
Beispiele: Quader und Würfel
Die Abwicklung eines Körpers zum Erhalt des Körpernetzes wird am Beispiel eines Quaders vorgeführt. Allgemeine Grundlagen zu Netzen werden zusammengefasst.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Winkel messen [8:02]
Das Geodreieck & Winkel messen
Zunächst werden einige Grundbegriffe des Geodreiecks eingeführt. Anschließend wird an einem Beispiel die Winkelmessung demonstriert. Dabei wird auf die beiden Winkelskalen am Geodreieck eingegangen und es werden zwei Varianten zur Winkelmessung dargestellt. Hierbei finden beide Skalen Anwendung zur Messung des Winkels.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Winkel zeichnen [3:45]
Anschaulich beschrieben wird die Vorgehensweise beim Zeichnen eines Winkels. Hierbei wird ein spitzer und ein stumpfer Winkel als Beispiel gezeichnet.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: [2:45]
Winkelsumme in Dreieck und Viereck
Die Winkelsumme in Dreieck und Viereck wird anschaulich dargestellt.
Geometrie: [2:14]
Grundkonstruktionen: Halbieren einer Strecke
Es wird die Halbierung einer Strecke konstruiert. Dabei entsteht die Mittelsenkrechte auf der Strecke zwischen den Punkten A und B.
Geometrie: [0:45]
Grundkonstruktionen - Halbieren eines Winkels
Technisches Zeichnen - Geometrie:
Grundkonstruktionen - Das gleichseitige Dreieck [1:38]
siehe auch: Themenseite - Technisches Zeichnen
Geometrie: Die Parallelverschiebung [5:55]
Zeichentechnik
Zeichentechnik für parallel verlaufende Strecken in einer Zeichnung.
Die Parallelverschiebung - Geometrische Anwendung:
Anwendung der Zeichentechnik [3:23]
Durch Anwendung der Zeichentechnik für parallel verlaufenden Strecken wird durch die Parallelverschiebung ein Dreieck abgebildet. Die Verschiebung ist dabei durch einen Verschiebungspfeil vorgegeben.
Geometrie: [1:38]
Grundkonstruktionen - Das gleichseitige Dreieck
Geometrie: [2:11]
Grundkonstruktionen - Fällen eines Lotes
Es wird das Lot durch einen Punkt auf einer Geraden konstruiert.
Geometrie: [3:03]
Grundkonstruktionen - Streckenteilung
Geometrie: [2:30]
Grundkonstruktionen - Der Goldene Schnitt
Geometrie: [0:52]
Grundkonstruktionen - Tangente durch einen Punkt auf der Kreislinie
Geometrie: [2:40]
Grundkonstruktionen - Tangente durch einen Punkt außerhalb der Kreislinie
Geometrie: Dreiecke [7:06]
Dreiecke → Inkreis - Umkreis - Schwerpunkt
Die Konstruktion von Inkreis, Umkreis und Schwerpunkt eines Dreiecks wird vorgeführt. Es wird dabei Bezug genommen auf die Grundkonstruktionen (vgl. verlinkte Videos).
Abonnieren:
Geometrie: Satz des Thales [3:57]
Rechtwinklige Dreiecke konstruieren, Beweis
Die Konstruktion rechtwinkliger Dreiecke auf Grundlage des Satzes von Thales wird demonstriert und anschließend der Satz anschaulich bewiesen.
Geometrie: Dreiecke [2:58]
Dreiecke konstruieren ( 1. Fall: SSS )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der erste Fall: SSS (Drei Seiten sind gegeben) - Kongruenzsätze
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Dreiecke [2:58]
Dreiecke konstruieren ( 2. Fall: SWS )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der zweite Fall: SWS (Zwei Seiten und der eingeschlossene Winkel sind gegeben) - Kongruenzsätze
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Dreiecke [3:04]
Dreiecke konstruieren ( 3. Fall: WSW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der dritte Fall: WSW - Kongruenzsätze
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Dreiecke [2:49]
Dreiecke konstruieren ( 4. Fall: SWW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der vierte Fall: SWW - Kongruenzsätze
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Dreiecke [4:10]
Dreiecke konstruieren ( 5. Fall: SSW )
Die Konstruktion von Dreiecken wird anhand eines Beispiels vorgeführt - hier der fünfte Fall: SSW - Kongruenzsätze
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Dreiecke [5:02]
Flächenberechnung am Dreieck
Gezeigt wird die Berechnung der Fläche eines allgemeinen Dreiecks.
Geometrie: Parallelogramm und Raute [4:17]
Flächenberechnung an Parallelogramm und Raute
Die Berechnung der Fläche eines Parallelogramms (bzw. einer Raute) wird durch einfache Symmetrieüberlegungen gezeigt.
Geometrie: Trapez [3:25]
Flächenberechnung am Trapez
Die Berechnung der Fläche eines Trapezes wird durch einfache Symmetrieüberlegungen gezeigt.
Geometrie: Der Kreis (1) [6:17]
Bestimmung des Kreisumfangs - Kreiszahl π (Pi) -
Beispielrechnungen
Die Formel zur Berechnung des Kreisumfangs wird anschaulich hergeleitet und die Kreiszahl Pi eingeführt. Anschließend werden zwei Anwendungsbeispiele vorgerechnet.
Geometrie: Der Kreis (2) [5:35]
Bestimmung der Kreisfläche: Herleitung und Beispielrechnungen
Die Formel zur Berechnung der Kreisfläche wird anschaulich hergeleitet. Anschließend werden zwei Anwendungsbeispiele vorgerechnet.
Geometrie: Der Kreis (3) [6:06]
Berechnung von Kreissektoren und Kreisbögen
Die Grundlagen zur Berechung von Kreisteilen (Kreissktoren und Kreisbögen) wird anschaulich demonstriert.
Anschließend werden Beispiele berechnet.
(Anmerkungen: radius → Radius ; diameter → Durchmesser ; perimeter → Umfang ; area → Fläche )
Geometrie: Zentrische Streckung [3:55]
Anschaulich vorgeführt wird am Beispiel eines Dreiecks die zentrische Streckung mit Streckfaktor 2,5.
Geometrie: Ähnlichkeit und Kongruenz [8:55]
Die Begriffe "Ähnlichkeit" und "Kongruenz" werden an einem Beispiel erklärt. Dabei wird auch unterschieden zwischen der gleichsinnigen und ungleichsinnigen Ähnlichkeit bzw. Kongruenz.
Geometrie: Strahlensätze [8:03]
Motivation, Beweis, Anwendung
Die Strahlensätze werden detailliert und schrittweise hergeleitet und anschließend ein Beispiel zur Anwendung gezeigt und vorgerechnet.
Geometrie: Der Satz des Pythagoras [7:11]
Motivation, Beweis, Anwendung
Der Satz des Pythagoras wird bewiesen. Die dadurch möglichen Dreiecksberechnungen als Grundlage für weiterführende Berechnungen werden demonstriert. Abschließend wird in einem einfachen Beispiel eine Anwendung des S.d.P. gezeigt.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Euklid: Höhensatz [3:20]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Höhensatzes des Euklid.
Geometrie: Euklid: Kathetensatz [4:37]
Anschauliche Herleitung
Anschaulich beschrieben wird der Beweis des Kathetensatzes des Euklid.
Geometrie: Möndchen des Hippokrates [5:08]
Möndchen des Hippokrates
Anschaulich beschrieben wird der Zusammenhang zwischen dem Flächeninhalt der "Möndchen des Hippokrates" und der zugehörigen Dreiecksfläche.
Geometrie: Der Zylinder (1) [8:52]
Die Oberflächenformel
Die Oberflächenformel für den Zylinder wird anschaulich hergeleitet. Anschließend werden die Ergebnisse in einer Übersicht zusammengefasst und noch ein Beispiel vorgerechnet.
Geometrie: Der Zylinder (2) [4:21]
Die Volumenformel
Die Volumenformel eines Zylinders wird anschaulich hergeleitet. Anschließend werden die Ergebnisse zusammengefasst und ein Beispiel vorgerechnet.
Geometrie: Die Pyramide [3:42]
Die Volumenformel
Anschaulich wird die Herleitung der Volumenformel für die Pyramide gezeigt.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Die Pyramide [3:11]
Die Oberfläche (1)
Beschrieben und veranschaulicht wird die Berechnung der Oberfläche einer Pyramide.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
Geometrie: Die Pyramide [3:39]
Die Oberfläche
(2) - Zusammenhang der Größen
Beschrieben und veranschaulicht werden die Zusammenhänge der charakteristischen Größen einer Pyramide zur Oberflächenberechnung.
Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung - Nicht kommerziell - Keine Bearbeitung.
