Digitaltechnik (1)
Hier findest du die Folien zur Unterrichtseinheit.
Inhalt - Digitaltechnik
Teil 1:
Analoge Darstellung
Digitale Darstellung
DIGITALE SIGNALE
Anwendungen im Alltag
Technische Umsetzungsmöglichkeiten
Logische Zustände: „0“ und „1“
ELEKTRIZITÄT (RÜCKBLICK)
SCHALTSYMBOLE
Elektrische Schaltsymbole
Digitale Schaltsymbole
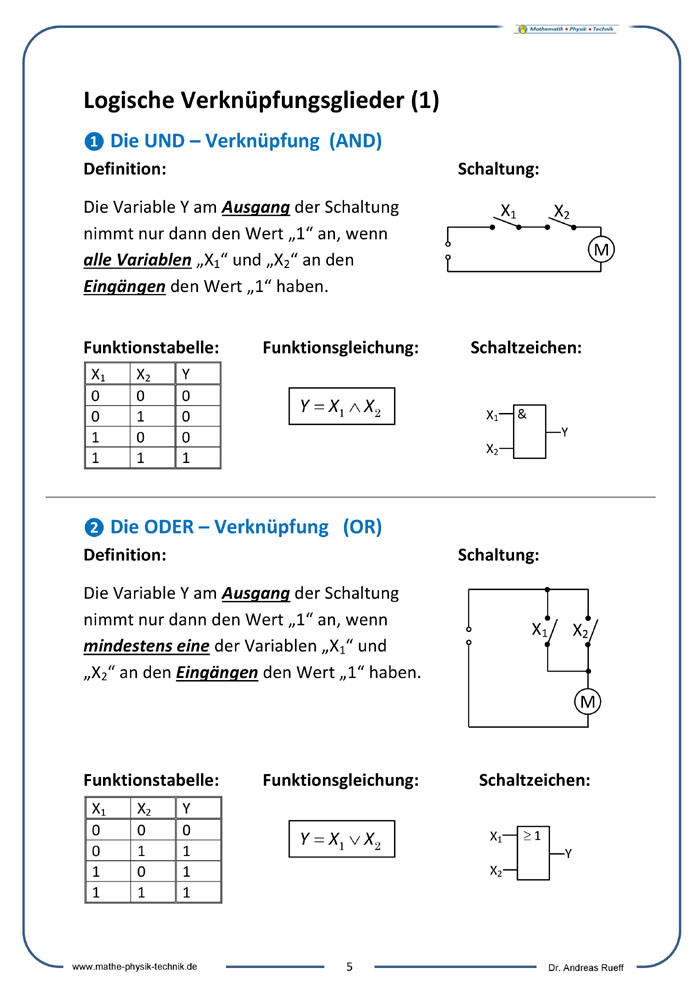
LOGISCHE VERKNÜPFUNGSGLIEDER
❶ Die UND – Verknüpfung (AND)
❷ Die ODER – Verknüpfung (OR)
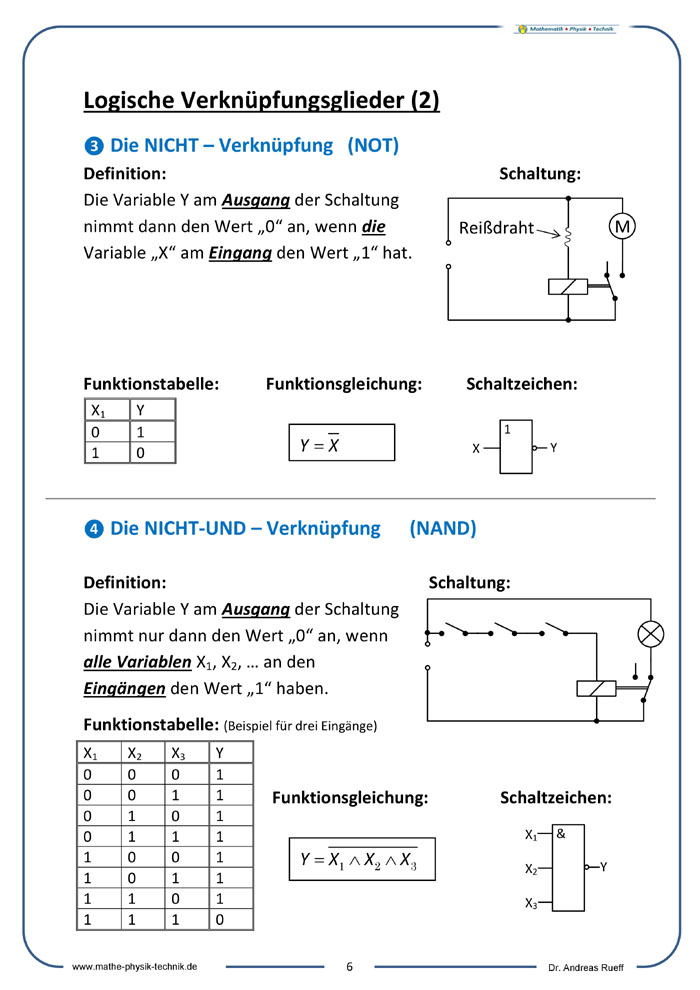
❸ Die NICHT – Verknüpfung (NOT)
❹ Die NICHT-UND – Verknüpfung (NAND)
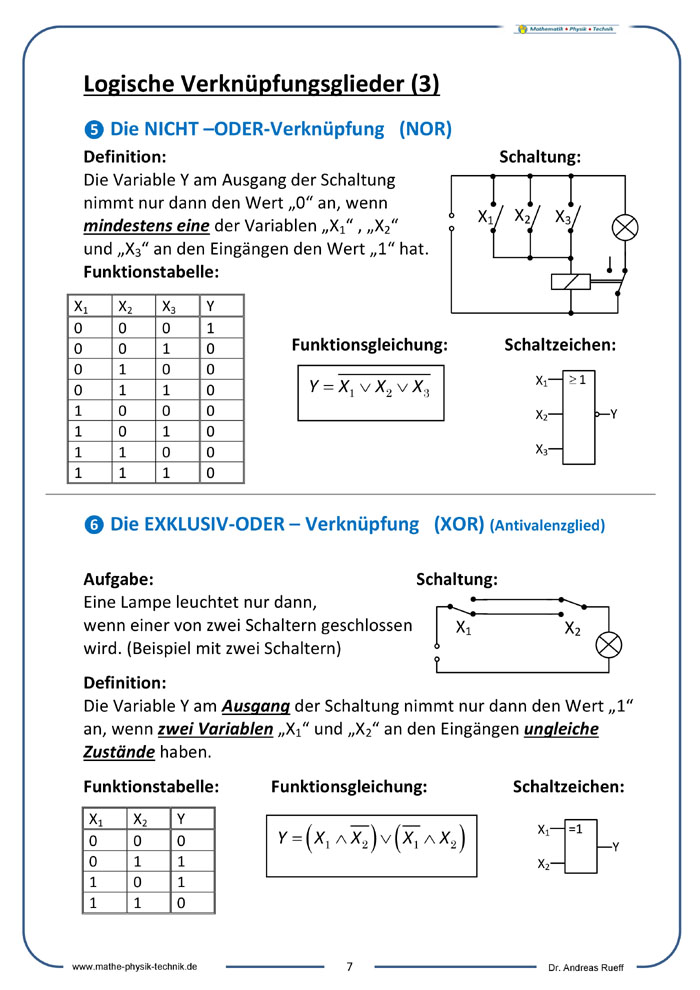
❺ Die NICHT –ODER-Verknüpfung (NOR)
❻ Die EXKLUSIV-ODER – Verknüpfung (XOR) (Antivalenzglied)
❼ Die ÄQUIVALENZ– Verknüpfung (XNOR) (Äquivalenzglied)
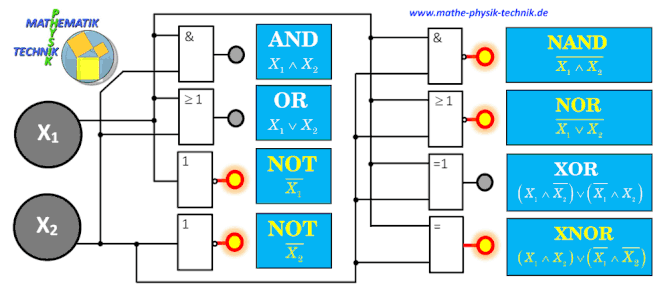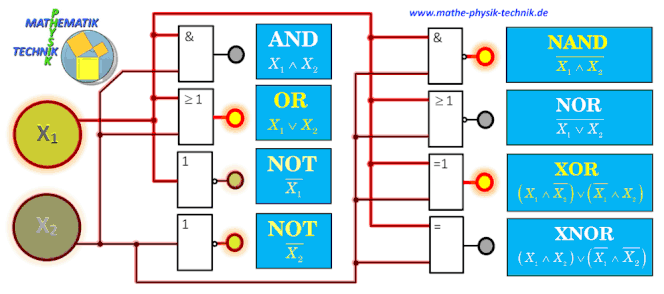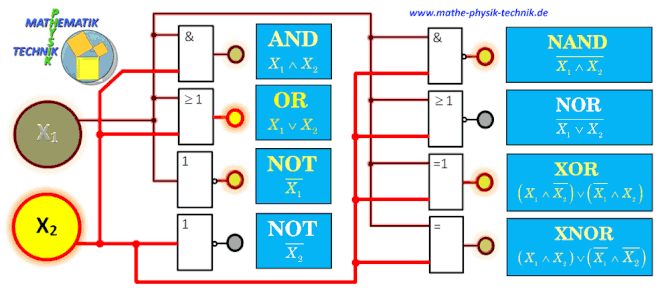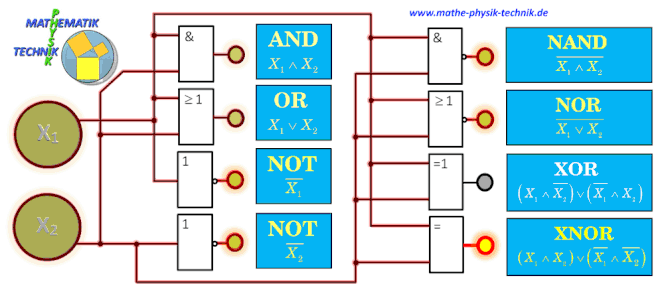
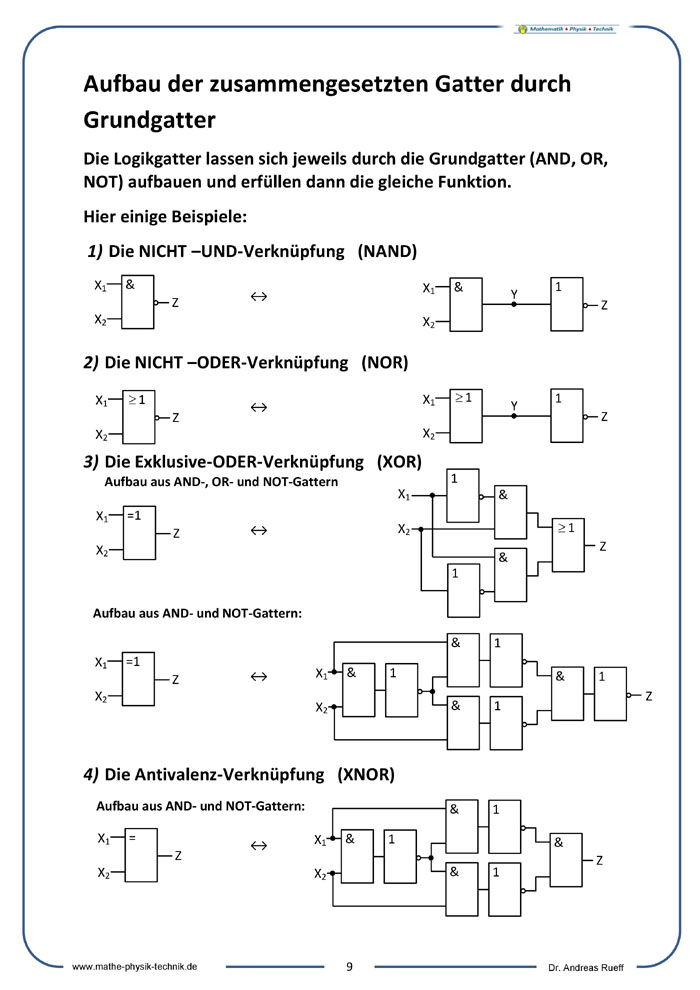
AUFBAU DER ZUSAMMENGESETZTEN GATTER DURCH GRUNDGATTER
SCHALTUNGSANALYSE
Welche Verknüpfung erzeugen einzelne Schaltungsteile?
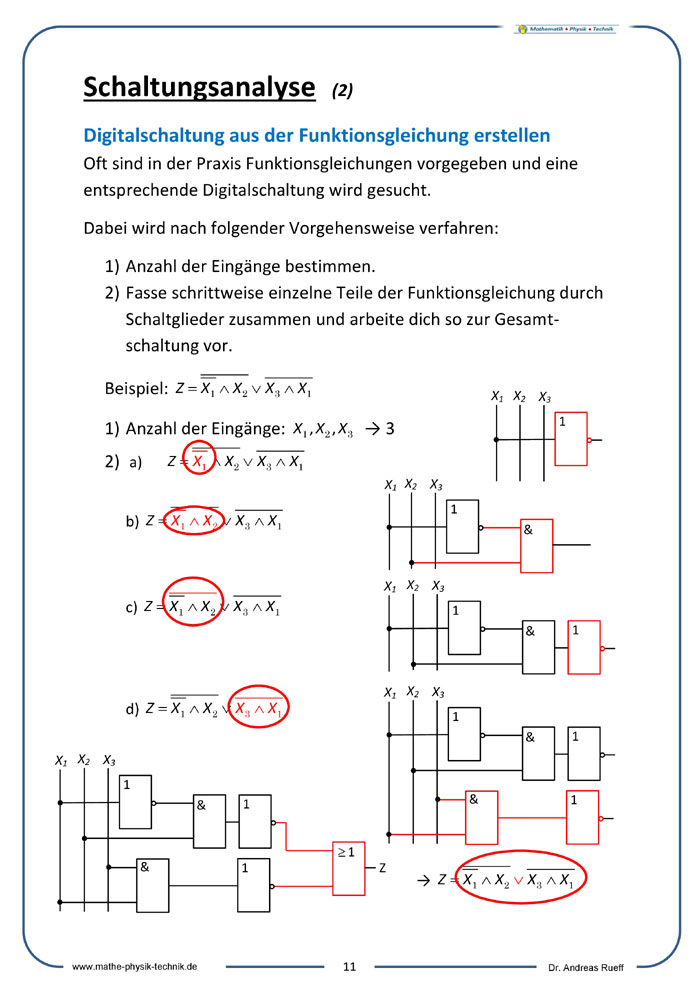
Digitalschaltung aus der Funktionsgleichung erstellen
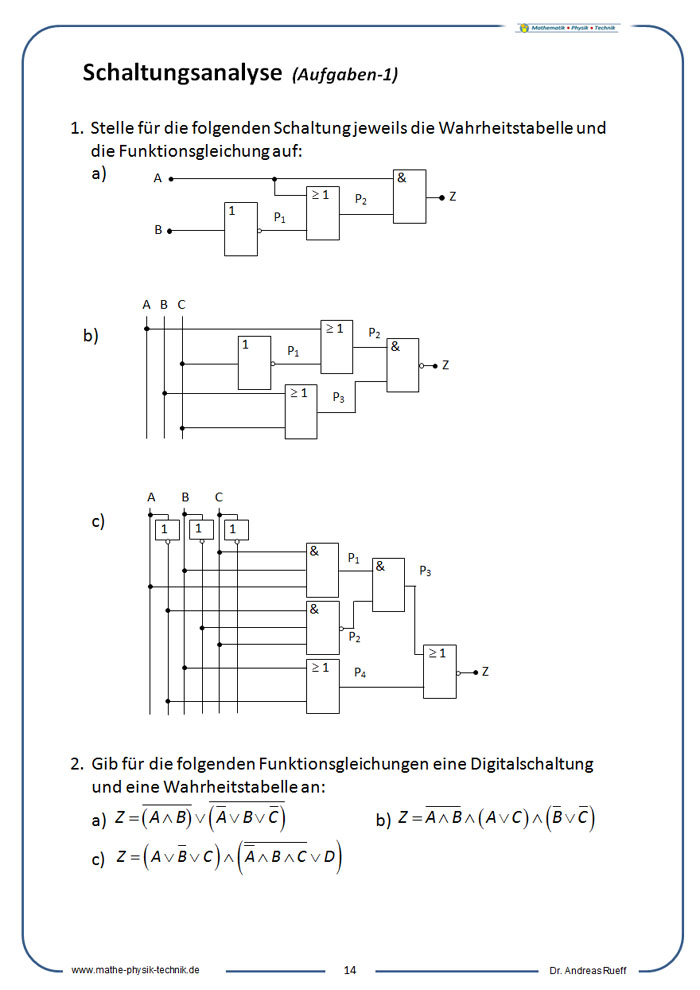
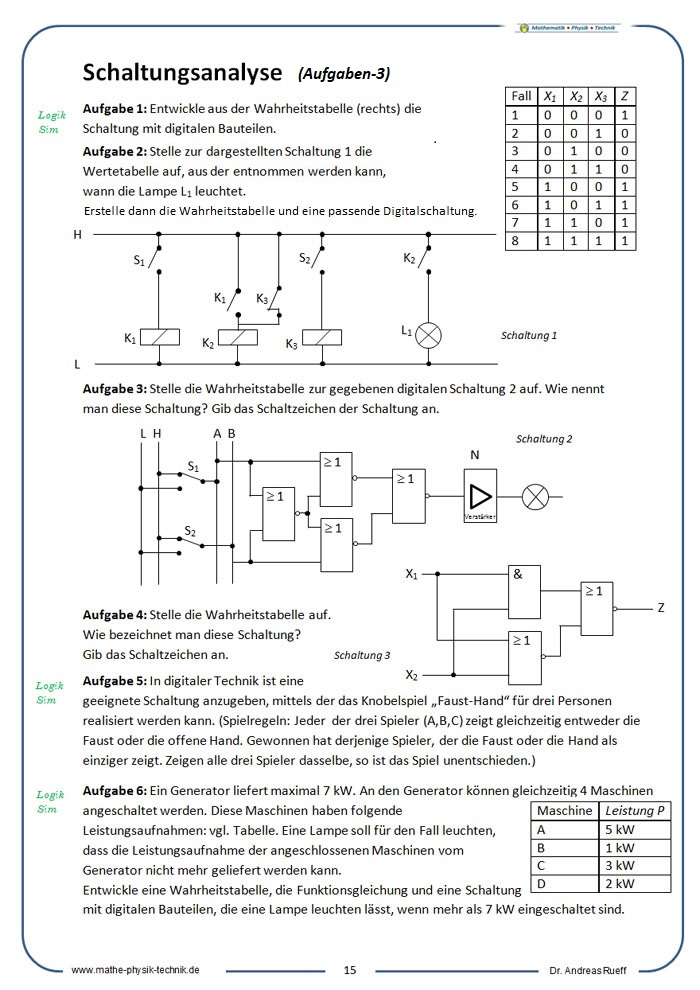
SCHALTUNGSANALYSE (AUFGABEN)
BOOLESCHE ALGEBRA
Vorüberlegungen
Grundgesetze der Schaltalgebra
❶ Grundgleichungen
❷ Rechenregeln mit einer Variablen
❸ Rechenregeln mit zwei und mehr Variablen
Morgansche Gesetze
Bindungsregeln
BOOLESCHE ALGEBRA (AUFGABEN 1)
Anwendung der Gesetzmäßigkeiten
BOOLESCHE ALGEBRA (AUFGABEN 2)
SCHALTUNGSSYNTHESE
Die ODER-Normalform
Vereinfachung der ODER-Normalform: KV-Diagramme
SCHALTUNGSSYNTHESE (AUFGABEN - 1)
SCHALTUNGSSYNTHESE (AUFGABEN - 2)
DATEN SPEICHERN
Das Flipflop
Funktionsweise – RS-Flipflop
Aufbau eines RS-Flipflops durch NAND-Glieder
RS-Flipflop mit dominierendem Eingang
Taktzustandsgesteuertes RS-Flipflop (Auffang-Flipflop)
D-Flipflop
Taktflankengesteuerte Flipflops
Taktflankengesteuertes RS-Flipflop
Taktflankengesteuertes D-Flipflop
Das Schieberegister
RECHENSCHALTUNGEN
Dualzahlen
Der Halbaddierer
Der Volladdierer (FA – engl. full adder)
Die Paralleladdierschaltung
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen
Einführung

Infotext - 01/02 - Darstellungsarten - Digital, Analog
In der realen, physischen Welt verhält sich Vieles stufenlos (kontinuierlich); Ursache und Wirkung sind direkt aneinander gekoppelt und verhalten sich damit wörtlich
„analog“ (von altgriechisch analogos „entsprechend, gleichartig, verhältnismäßig, passend, ähnlich“).
Seit dem letzten 20. Jahrhundert wurden zunehmen digitale Technologien entwickelt, mit denen sich manche Aufgaben leichter und besser lösen lassen. In der Digitaltechnik
werden alle ursprünglich kontinuierlichen Werte quantisiert und zugleich zeitlich diskretisiert. Das bedeutet, sie werden in ihrem Wert als auch dem
Zeitpunkt des Auftretens gerastert. Benachbarte Werte sind also stufenweise voneinander getrennt.
Ein Beispiel ist die Darstellung eines Bildes auf einem Bildschirm. Zoomen wir an das Bild heran, um sehr keine Details zu erkennen, dann sehen wir irgendwann nur noch quadratische
Kästchen. Beim Original ist eine derartige Rasterung natürlich nicht sichtbar.

Durch die stufenweise Trennung einzelner Bereiche geht der analoge Charakter verloren. Die direkte kontinuierliche Verknüpfung des Eingangs- und Ausgangssignals, also beim Übertrag des Originals auf die Abbildung des Gemäldes, wird aufgehoben. Dabei geht zwar Information verloren, weil kleine Nuancen und Änderungen eines Signals nicht immer beachtet werden – doch diese Signale können leichter verarbeitet und übertragen werden. Durch die sich ergebenden Abstufungen entsteht z. B. die Möglichkeit, Fehler bei der Übertragung vollständig zu elimieren, weil kleine Einflüsse auf Wert und Zeitpunkte nicht zu einem „Verlassen“ des Rasters führen.
Um die Ergebnisse dieses Vorgangs wieder in der realen Welt nutzen zu können, ist oft auch wiedereine Umwandlung zurück in die analoge Form nötig (Mikrofon mit Analog-Digital-Umsetzer → Speicherung → Lautsprecher mit Digital-Analog-Umsetzer). Das einfachste Beispiel für analog und digital ist eine Rampe und eine Treppe. Natürlich kann man mit steigendem Aufwand die Stufen der Treppe immer kleiner machen, bis der Unterschied unkenntlich wird. Seit 1950 kann man diese Fortschritte am deutlichsten am Leistungsumfang von Mikroprozessoren in Computern nachvollziehen.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Was ist der Unterschied zwischen analogen und digitalen Daten?
3) → Meilensteine - Blaise Pascal und der Druck
4) → Meilensteine des Wissens - Meisterwerke der Kunst: Pascaline
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Aufgaben:

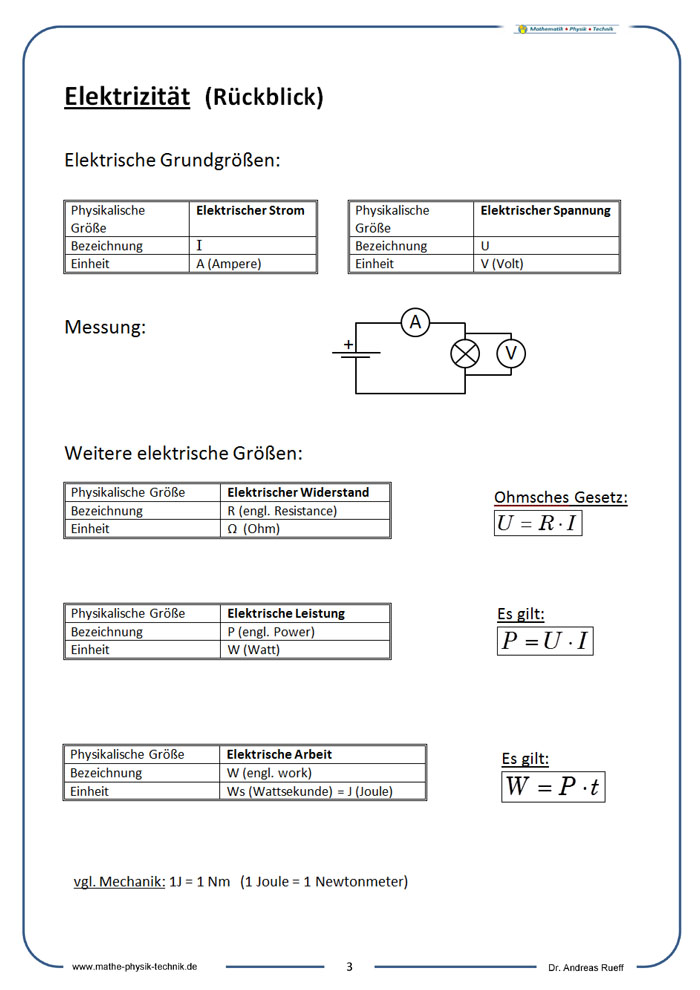
→ siehe auch: Themenseite Elektrizitätslehre
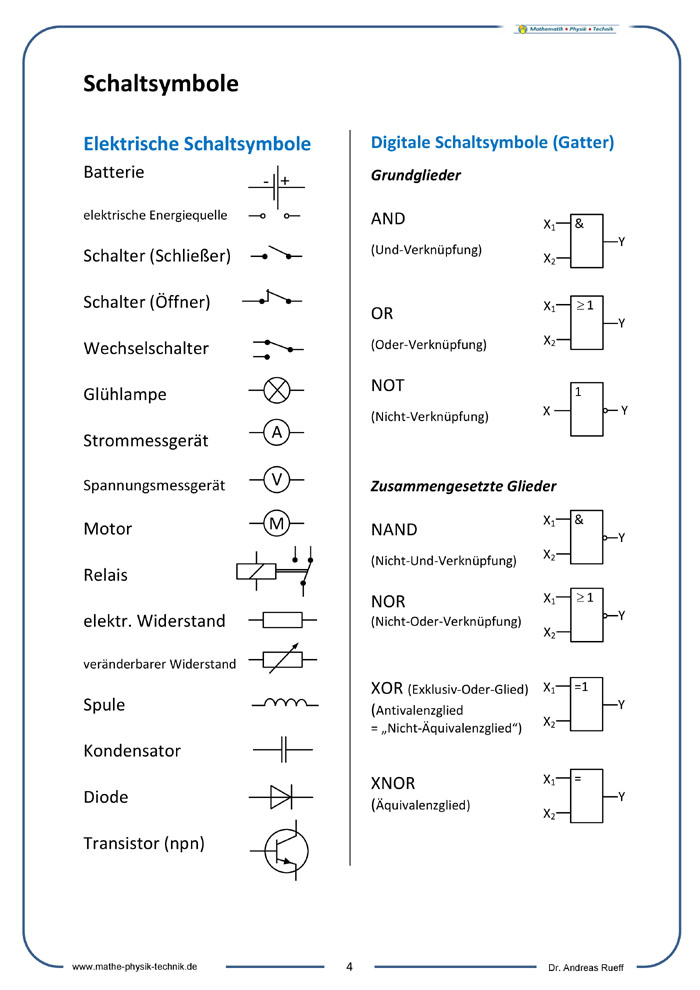
Infotext - 04 - Elektrische und digitale Schaltsymbole
Logische Verknüpfungen - Schaltsymbole [04]
Ein Logikgatter, auch nur Gatter, ist eine Anordnung die binäre Eingangssignale zu einem binären Ausgangssignal verarbeitet. Ein oder auch mehrere Eingangssignale werden zu einem einzigen logischen Ergebnis umgewandelt und auf das Ausgangssignal abgebildet.
 Geschichte
Geschichte
Mathematisch exakt wurde das Binärsystem zuerst von Gottfried Wilhelm Leibniz beschrieben (Veröffentlichung im Jahre 1705).
Die ersten Logikgatter wurden noch mechanisch realisiert. 1837 entwarf der englische Erfinder Charles Babbage mit der Analytical Engine eine erste vollautomatische
Rechenmaschine, die heute als wichtiger Schritt in der Geschichte des Computers gilt. Seine „logischen Gatter“ arbeiteten auf Grundlage mechanischer Reaktionen.
Logische Verknüpfungen (Gatter)
Logische Operatoren sind die UND-Verknüpfung (Und-Gatter, Konjunktion), die ODER-Verknüpfung (Oder-Gatter, Disjunktion), die
NICHT-Verknüpfung (NICHT-Gatter, Negation) oder die EXKLUSIV-ODER-Verknüpfung (Exklusiv-Oder-Gatter, Kontravalenz). Neben den genannten
Gatterfunktionen sind auch die Entsprechungen mit negiertem Ausgang (Das bedeutet, dass immer das Gegenteil des eigentlichen Ergebnisses ausgegeben wird) zu nennen:
NAND-Verknüpfung (Nicht-Und), NOR-Verknüpfung (Nicht-Oder), XNOR-Verknüpfung (Nicht-Exklusiv-Oder); deutsche Bezeichnungen der
letztgenannten Gatter sind unüblich.
Prinzipiell lassen sich alle logischen Verknüpfungen als Gatter realisieren. Mehrere Logikgatter kann man zusammenschalten und Datenspeicher und Zähler
erstellen. Aus mehreren dieser Schaltungen lassen sich weiterhin zum Beispiel Mikroprozessoren zusammenstellen. Einzelne Logikgatter werden als integrierter
Schaltkreis (IC) angeboten; in komplexeren Schaltungen kommen sie mitunter innerhalb eines ICs zig-millionenfach vor. Sie lassen sich aber auch aus diskreten elektronischen
Bauelementen, mittels Schalter oder Relais aufbauen. Ebenfalls gibt es in historischen Rechenmaschinen mechanische Aufbauten (s.o.: Analytical Engine).
Zur Vereinfachung einer komplexen logischen Funktion wird die so genannte Schaltalgebra angewandt. Die Schaltnetze, die man mithilfe der Schaltalgebra berechnet, wurden
früher hauptsächlich in elektromechanischen Bauweisen hergestellt. In der Regel wird hierbei dem Schalterzustand „aus“ eine logische Null „0“ zugeordnet, dem Schalterzustand
„ein“ entsprechend eine logische Eins „1“.
In der heutigen Digitaltechnik baut man binäre Schaltsysteme überwiegend aus elektronischen Bauelementen auf. Hierbei werden die logischen Zustände durch unterschiedliche
Spannungen realisiert.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Die wichtigsten Logischen Gatter UND ODER NOR NAND - E-Technik in 5 Min.
2) → UND - Verknüpfung / Digitaltechnik / Wahrheitstabelle ...
3) → ODER - Verknüpfung / Digitaltechnik / Wahrheitstabelle ...
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Logische Verknüpfungen
Infotext - Logische Verknüpfungen [05-09]
Ein Logikgatter, auch nur Gatter, ist eine Anordnung die binäre Eingangssignale zu einem binären Ausgangssignal verarbeitet. Ein oder auch mehrere Eingangssignale werden zu einem einzigen logischen Ergebnis umgewandelt und auf das Ausgangssignal abgebildet.
 Geschichte
Geschichte
Mathematisch exakt wurde das Binärsystem zuerst von Gottfried Wilhelm Leibniz beschrieben (Veröffentlichung im Jahre 1705).
Die ersten Logikgatter wurden noch mechanisch realisiert. 1837 entwarf der englische Erfinder Charles Babbage mit der Analytical Engine eine erste vollautomatische
Rechenmaschine, die heute als wichtiger Schritt in der Geschichte des Computers gilt. Seine „logischen Gatter“ arbeiteten auf Grundlage mechanischer Reaktionen.
Logische Verknüpfungen (Gatter)
Logische Operatoren sind die UND-Verknüpfung (Und-Gatter, Konjunktion), die ODER-Verknüpfung (Oder-Gatter, Disjunktion), die
NICHT-Verknüpfung (NICHT-Gatter, Negation) oder die EXKLUSIV-ODER-Verknüpfung (Exklusiv-Oder-Gatter, Kontravalenz). Neben den genannten
Gatterfunktionen sind auch die Entsprechungen mit negiertem Ausgang (Das bedeutet, dass immer das Gegenteil des eigentlichen Ergebnisses ausgegeben wird) zu nennen:
NAND-Verknüpfung (Nicht-Und), NOR-Verknüpfung (Nicht-Oder), XNOR-Verknüpfung (Nicht-Exklusiv-Oder); deutsche Bezeichnungen der
letztgenannten Gatter sind unüblich.
Prinzipiell lassen sich alle logischen Verknüpfungen als Gatter realisieren. Mehrere Logikgatter kann man zusammenschalten und Datenspeicher und Zähler
erstellen. Aus mehreren dieser Schaltungen lassen sich weiterhin zum Beispiel Mikroprozessoren zusammenstellen. Einzelne Logikgatter werden als integrierter
Schaltkreis (IC) angeboten; in komplexeren Schaltungen kommen sie mitunter innerhalb eines ICs zig-millionenfach vor. Sie lassen sich aber auch aus diskreten elektronischen
Bauelementen, mittels Schalter oder Relais aufbauen. Ebenfalls gibt es in historischen Rechenmaschinen mechanische Aufbauten (s.o.: Analytical Engine).
Zur Vereinfachung einer komplexen logischen Funktion wird die so genannte Schaltalgebra angewandt. Die Schaltnetze, die man mithilfe der Schaltalgebra berechnet, wurden
früher hauptsächlich in elektromechanischen Bauweisen hergestellt. In der Regel wird hierbei dem Schalterzustand „aus“ eine logische Null „0“ zugeordnet, dem Schalterzustand
„ein“ entsprechend eine logische Eins „1“.
In der heutigen Digitaltechnik baut man binäre Schaltsysteme überwiegend aus elektronischen Bauelementen auf. Hierbei werden die logischen Zustände durch unterschiedliche
Spannungen realisiert.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Die wichtigsten Logischen Gatter UND ODER NOR NAND - E-Technik in 5 Min.
2) → UND - Verknüpfung / Digitaltechnik / Wahrheitstabelle ...
3) → ODER - Verknüpfung / Digitaltechnik / Wahrheitstabelle ...
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Hinweis: Es bleiben zwei Kärtchen übrig.
Diese App wurde erstellt von Thomas Fecker bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!


Diese App ist ein Derivat einer App von inf schule bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist ein Derivat einer App von inf schule bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
LogikSim: → Link zur Anbieterseite
LogikSim wurde in Delphi für den Lehrgebrauch geschrieben und ermöglicht es logische Schaltungen zu entwerfen und zu testen. Es ist ein OpenSource-Projekt und darf daher kostenlos genutzt werden. Ein Hauptziel war es, eine intuitive und übersichtliche Bedienung zu ermöglichen.
Videos:
1) → LogikSim Grundlagen [German] [HD]
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
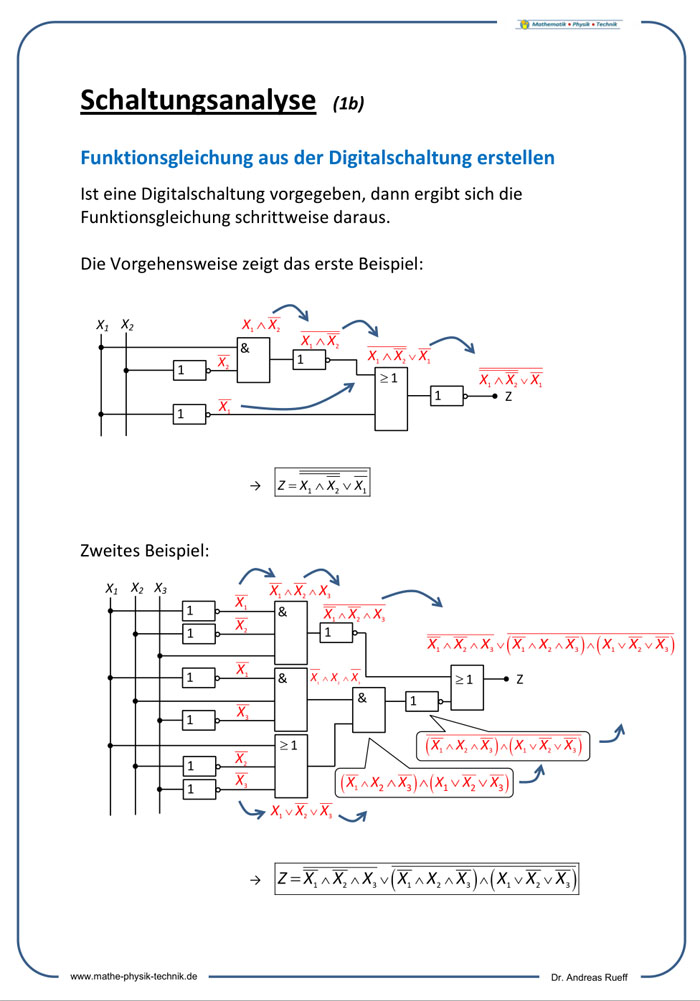
Schaltungsanalyse


Konrad Zuse
Konrad Ernst Otto Zuse (1910 - 1995) war ein deutscher Bauingenieur, Erfinder und Unternehmer (Zuse KG). Mit seiner Entwicklung der Z3 im Jahre 1941 baute Zuse den ersten funktionsfähigen
Computer der Welt.
 Konrad Zuse wurde als Sohn von Maria
und Emil Zuse geboren. Zuse hat sich selbst als „Bummelstudent“ bezeichnet. Als 17-Jähriger studierte er an der Technischen Hochschule Berlin-Charlottenburg (heute Technische Universität
Berlin) zunächst Maschinenbau, wechselte dann zur Architektur und schließlich zum Bauingenieurswesen. 1935 schloss Zuse sein Ingenieurstudium mit einem Diplom ab. Danach arbeitete er
zunächst als Statiker bei der Henschel Flugzeug-Werke AG in Schönefeld bei Berlin, gab diese Stelle jedoch bald auf und richtete eine Erfinderwerkstatt in der Wohnung seiner Eltern ein.
Hier entstand die Z1, eine programmierbare Rechenmaschine, die allerdings noch nicht voll funktionsfähig war, weil sie mechanisch funktionierte. Das Prinzip der Z1 übernahm Zuse dann für
die Z3, die er mit Relais aufbaute. Dies war der erste voll funktionsfähige Computer der Welt. Zuse verfügte über die Gabe, Menschen mit seiner Begeisterung so anzustecken, dass sie ihm
immer wieder Geld gaben – sein Vater ließ sich sogar aus dem Ruhestand reaktivieren, um die Entwicklung mitzufinanzieren – oder Arbeitszeit spendeten.
Konrad Zuse wurde als Sohn von Maria
und Emil Zuse geboren. Zuse hat sich selbst als „Bummelstudent“ bezeichnet. Als 17-Jähriger studierte er an der Technischen Hochschule Berlin-Charlottenburg (heute Technische Universität
Berlin) zunächst Maschinenbau, wechselte dann zur Architektur und schließlich zum Bauingenieurswesen. 1935 schloss Zuse sein Ingenieurstudium mit einem Diplom ab. Danach arbeitete er
zunächst als Statiker bei der Henschel Flugzeug-Werke AG in Schönefeld bei Berlin, gab diese Stelle jedoch bald auf und richtete eine Erfinderwerkstatt in der Wohnung seiner Eltern ein.
Hier entstand die Z1, eine programmierbare Rechenmaschine, die allerdings noch nicht voll funktionsfähig war, weil sie mechanisch funktionierte. Das Prinzip der Z1 übernahm Zuse dann für
die Z3, die er mit Relais aufbaute. Dies war der erste voll funktionsfähige Computer der Welt. Zuse verfügte über die Gabe, Menschen mit seiner Begeisterung so anzustecken, dass sie ihm
immer wieder Geld gaben – sein Vater ließ sich sogar aus dem Ruhestand reaktivieren, um die Entwicklung mitzufinanzieren – oder Arbeitszeit spendeten.
Z1 – ein „mechanisches Gehirn“
Da die statischen Berechnungen im Bauingenieurwesen sehr monoton und mühselig waren, kam Zuse die Idee, diese zu automatisieren. Er kündigte 1935 seine Statiker-Tätigkeit und widmete sich
ausschließlich der Umsetzung seiner Pläne, die er in einem Tagebucheintrag vom Juni 1937 beschreibt: „Seit etwa einem Jahr beschäftige ich mich mit dem Gedanken des mechanischen Gehirns.“
Das Resultat war der 1938 fertiggestellte, elektrisch angetriebene mechanische Rechner Z1. Er arbeitete als erster Rechner mit binären Zahlen und einen Programmwerk, das die Programme von
gelochten Kinofilmstreifen ablas. Die Z1 arbeitete aufgrund von Problemen mit der mechanischen Präzision nie zuverlässig; die mechanischen Schaltwerke klemmten regelmäßig. Noch während er
an der Z1 arbeitete, übertrug er die mechanische Schaltung in die elektromechanische Relaistechnik. Dies führte 1939 zu einem Prototyp Z2.
Z3 – der erste funktionsfähige Computer der Welt
1941 baute Zuse in den Räumen des Ingenieurbüros, das er inzwischen gegründet hatte, die Z3. Am 12. Mai 1941 stellte Zuse diese Rechenmaschine Z3 vor. Es war ein vollautomatisch
arbeitender Rechner mit Speicher und einer Zentralrecheneinheit aus Telefonrelais. Die Z3 gilt heute als erster funktionstüchtiger Computer der Welt. Das Gerät wurde praktisch zur
Berechnung einer komplexen Matrix eingesetzt, die zur Untersuchung des Flügelflatterns, das zum Absturz zahlreicher Flugzeuge geführt hatte, benötigt wurde. Allerdings wurde die Z3 nie
als „dringlich“ eingestuft und auch nie in den Routinebetrieb übernommen.
Z4 – Grundlage einer deutschen Computerindustrie
Auch die Weiterentwicklung der Z3 wurde von der Deutschen Versuchsanstalt für Luftfahrt gefördert. Es handelte sich auch bei dieser Entwicklung um einen aus Relais aufgebauten
elektromechanischen Rechner. Bis dahin waren sämtliche Rechner aus der Zuse-Produktion mit dem Anfangsbuchstaben Z wie „Zuse“ benannt worden. 1949 reiste Professor Eduard Stiefel von der
ETH Zürich in das Allgäu, um Zuse zu treffen und sich die Eignung der Z4 für Forschungen an der Universität demonstrieren zu lassen. Stiefel zeigte sich begeistert und einigte sich mit
Zuse über einen Mietvertrag zur Nutzung der Z4. Mit diesen finanziellen Mitteln war Zuse noch im selben Jahr im Stande, die Zuse KG zu gründen. Als 1950 die Z4 nach Zürich gebracht und an
der ETH eingesetzt wurde, war sie zu diesem Zeitpunkt der einzige funktionierende Computer in Mitteleuropa und der erste kommerzielle Computer weltweit.
Scheitern des Patentanspruchs
Zuse hatte schon vor dem Krieg mehrere Patente angemeldet. Am wichtigsten war jedoch eine Patentanmeldung von 1941, in der er die Z3 beschrieb. Die deutschen Prüfer hatten gegen Zuses
Ansprüche keine Einwände, und das Patent wurde 1952 bekanntgemacht. Dagegen erhoben Triumph, später auch IBM Einspruch. Der Prozess zog sich durch sämtliche Instanzen, bis das
Bundespatentgericht 1967 zur endgültigen Entscheidung kam, dass dem Erfinder des Computers „mangels Erfindungshöhe“ kein Patent erteilt werden könne.
Zuse KG
Nach dem Krieg gründete Zuse 1949 in Neukirchen im damaligen Kreis Hünfeld die Zuse KG. Weitere Computer wurden gebaut, die Typenbezeichnung war immer ein Z und eine fortlaufende Nummer.
Herausragend war die noch in Relaistechnik ausgeführte Z11, die der optischen Industrie, Universitäten und Flurbereinigungsbehörden verkauft wurde. Mit der Einführung der Elektronik
begann eine neue Zählung, und die Z22 wurde 1955 zum ersten in Röhrentechnik aufgebauten Computer von Zuse. Die Daten wurden in einem Magnetspeicher gespeichert.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
-
Konrad Zuse und seine ersten Computer der Welt - Fernsehbericht von 1958 [6:42]
-
Doku Die Zuse Story Wie ein Deutscher den Computer erfand deutsch [29:03]
-
[Doku] Digitale Verlustzone - Wie Deutschland den Anschluss an die Digitalisierung verlor [44:04]
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Fragen zum Text:
- Welches Fach studierte Konrad Zuse und wann beendete er sein Studium?
- Zuse erfand die „Z1“, eine programmierbare Rechenmaschine, die allerdings noch nicht voll funktionsfähig war. Warum war diese nicht voll funktionsfähig?
- Aus welchem Grund fing Zuse mit dem Bau der Z1 an?
- Die Z1 arbeitete mit Programmen (Software). Wie wurden diese „gespeichert“?
- Wann wurde die weiterentwickelte „Z3“ vorgestellt?
- Aus welchen Bauteilen wurde bei der „Z3“ die Zentralrecheneinheit aufgebaut?
- Wofür wurden die Berechnungen mit der „Z3“ benötigt?
- Wie konnte Zuse die Gründung der Zuse AG finanzieren?
- Aus welchem Grund wurde Zuse die Patentanmeldung für die Z3 verweigert?

Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hier einige Links die dich auch interessieren könnten:

Das Wissenschaftsjahr 2014 widmet sich der digitalen Revolution und ihren Folgen für unsere Gesellschaft. Wie verändern die digitalen Technologien unseren Alltag? Wie sieht die Zukunft unserer Kommunikation, Industrie und Arbeitswelt aus? Hier erfahren Sie mehr über die Hintergründe und Initiatoren des Jahres.

Das Bundesamt für Sicherheit in der Informationstechnik (BSI)
Wie mache ich meinen PC sicher? Welche Gefahren begegnen mir im Netz? Wie bewege ich mich sicher im Internet und im mobilen Netz? Das Bundesamt für Sicherheit in der Informationstechnik (BSI) ist der zentrale IT-Sicherheitsdienstleister des Bundes. Das BSI trägt dazu bei, die IT-Sicherheit in Deutschland zu erhöhen.

Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hinweis: Es werden keine Bücher oder sonstige, hier benannte Materialien im Unterricht verwendet oder benötigt.
Quellenangaben zu den Inhalten auf dieser Seite
Infotext ([01/02] Digital-Analog)
 Dieser Text basiert auf den Artikeln Digitaltechnik, Analogtechnik und Analog aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Digitaltechnik, Analogtechnik und Analog aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([04] Logische Verknüpfungen - Schaltsymbole)
 Dieser Text basiert auf den Artikeln Logikgatter und Analg aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der
Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist
eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Logikgatter und Analg aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der
Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist
eine Liste der Autoren verfügbar.
Die Abbildung wurde aus Wikimedia Commons entnommen: Datei : Babbages Analytical
Engine, 1834-1871. (9660574685).jpg
Infotext ( Digitaltechnik (Zusatz) - Konrad Zuse)
 Dieser Text basiert auf dem Artikel Konrad Zuse aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Konrad Zuse aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Die Abbildungen wurde aus Wikimedia Commons entnommen:
File:Konrad Zuse (1992).jpg
File:Zuse-Z4-Totale deutsches-museum.jpg
Hintergrundbild: Erstellt von A. Rueff unter Verwendung von zwei Vorlagen von Pixabay:
1. Bild von Gerd Altmann auf Pixabay
2. Bild von Gerd Altmann auf
Pixabay