Digitaltechnik (2)
Hier findest du die Folien zur Unterrichtseinheit.
Inhalt - Digitaltechnik
Analoge Darstellung
Digitale Darstellung
DIGITALE SIGNALE
Anwendungen im Alltag
Technische Umsetzungsmöglichkeiten
Logische Zustände: „0“ und „1“
ELEKTRIZITÄT (RÜCKBLICK)
SCHALTSYMBOLE
Elektrische Schaltsymbole
Digitale Schaltsymbole
LOGISCHE VERKNÜPFUNGSGLIEDER
❶ Die UND – Verknüpfung (AND)
❷ Die ODER – Verknüpfung (OR)
❸ Die NICHT – Verknüpfung (NOT)
❹ Die NICHT-UND – Verknüpfung (NAND)
❺ Die NICHT –ODER-Verknüpfung (NOR)
❻ Die EXKLUSIV-ODER – Verknüpfung (XOR) (Antivalenzglied)
❼ Die ÄQUIVALENZ– Verknüpfung (XNOR) (Äquivalenzglied)
AUFBAU DER ZUSAMMENGESETZTEN GATTER DURCH GRUNDGATTER
SCHALTUNGSANALYSE
Welche Verknüpfung erzeugen einzelne Schaltungsteile?
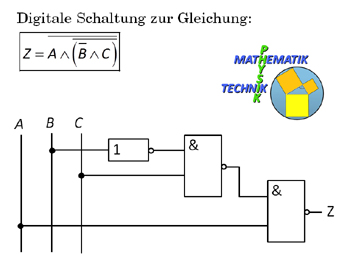
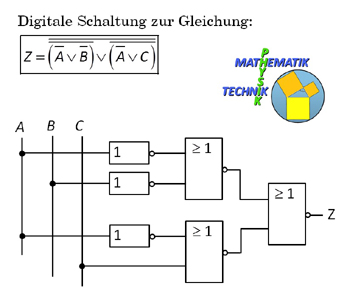
Digitalschaltung aus der Funktionsgleichung erstellen
SCHALTUNGSANALYSE (AUFGABEN)
Teil 2:
BOOLESCHE ALGEBRA
Vorüberlegungen
Grundgesetze der Schaltalgebra
❶ Grundgleichungen
❷ Rechenregeln mit einer Variablen
❸ Rechenregeln mit zwei und mehr Variablen
Morgansche Gesetze
Bindungsregeln
BOOLESCHE ALGEBRA (AUFGABEN 1)
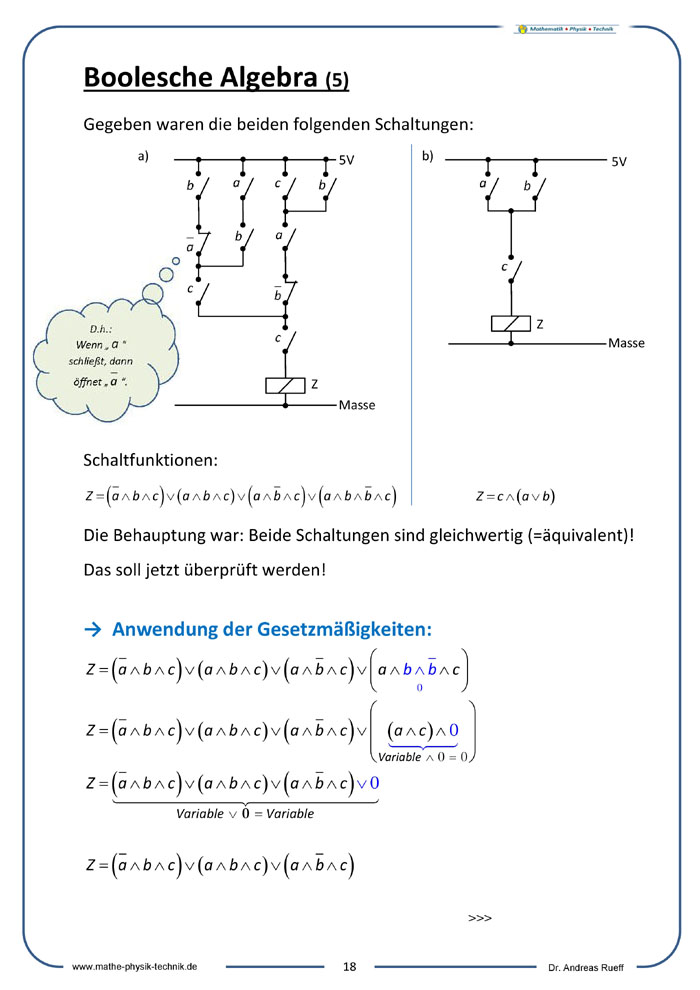
Anwendung der Gesetzmäßigkeiten
BOOLESCHE ALGEBRA (AUFGABEN 2)
SCHALTUNGSSYNTHESE
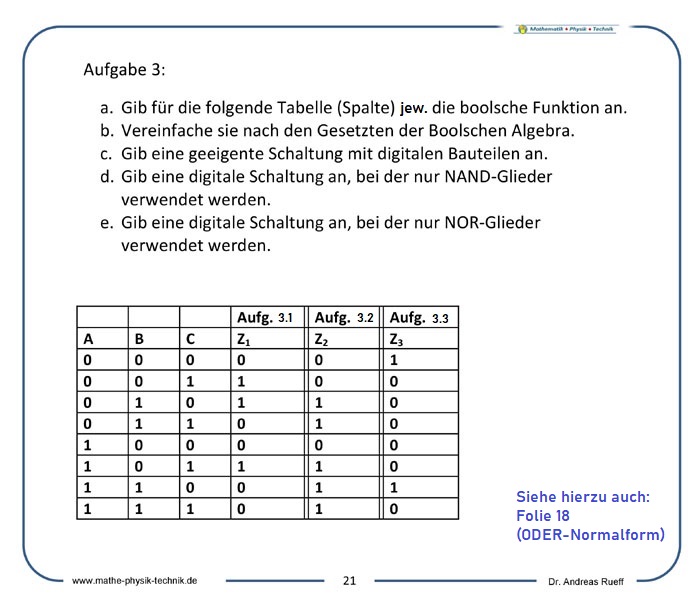
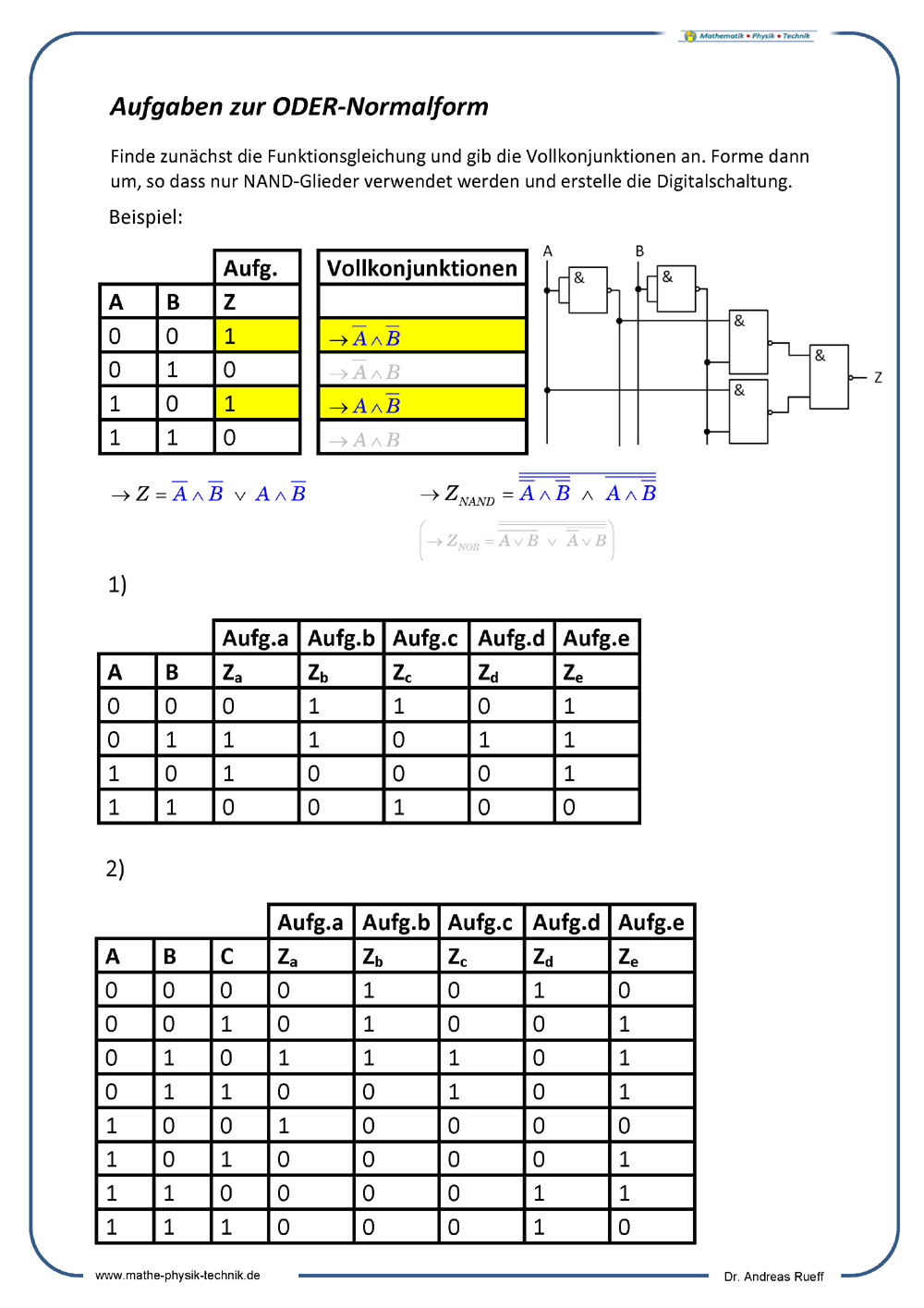
Die ODER-Normalform
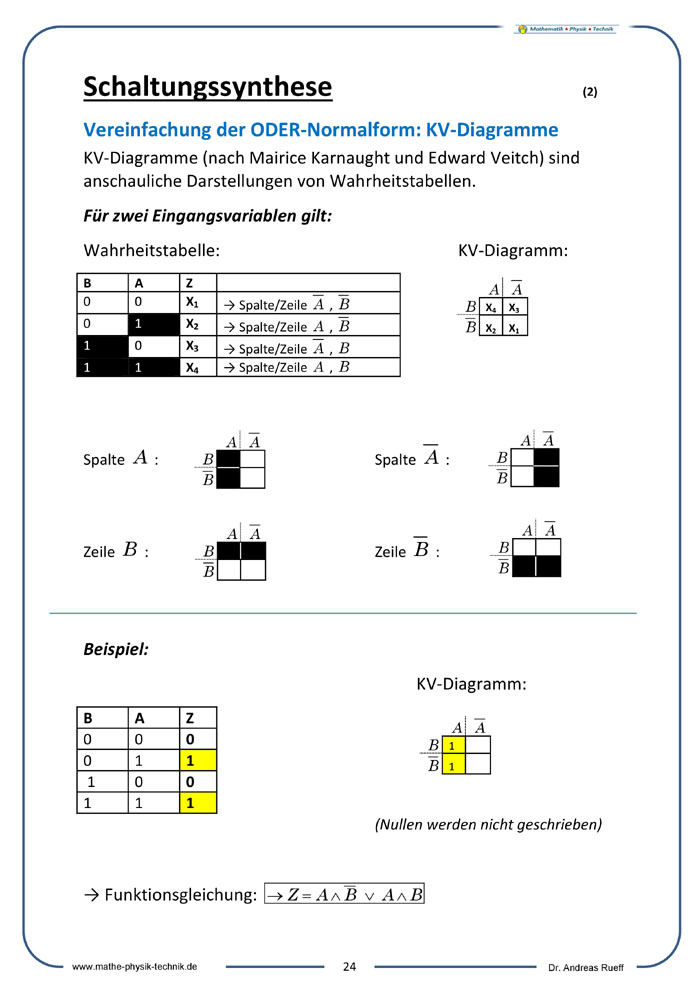
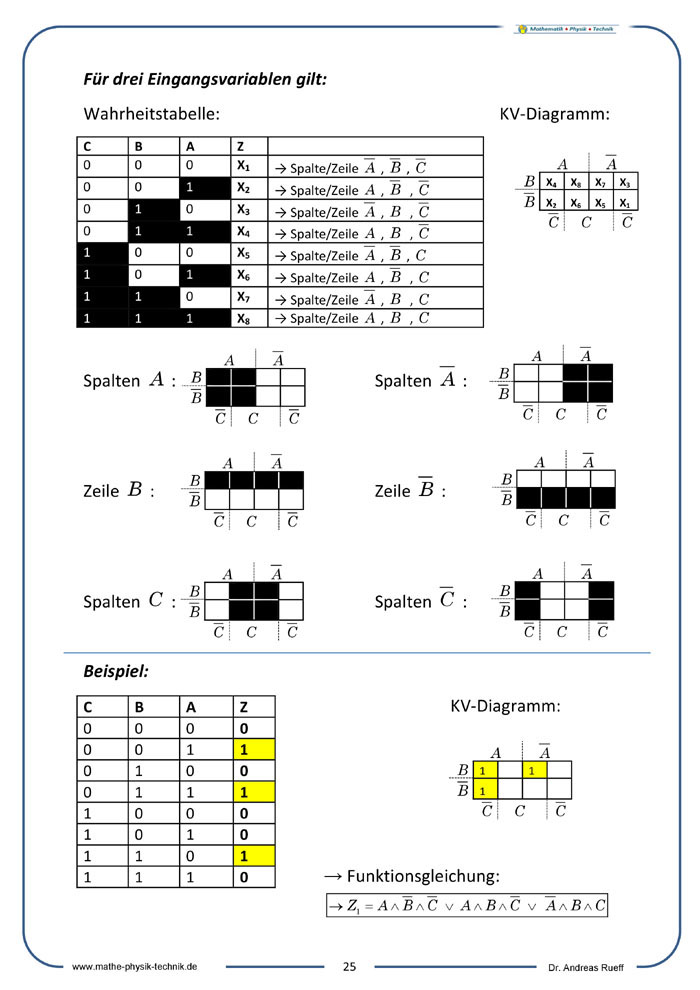
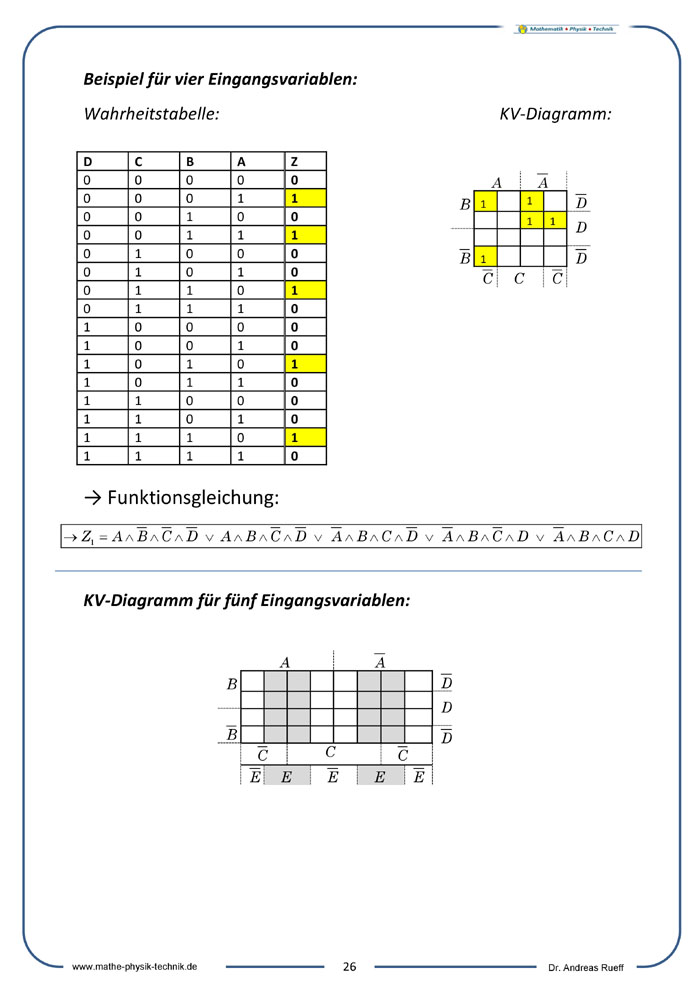
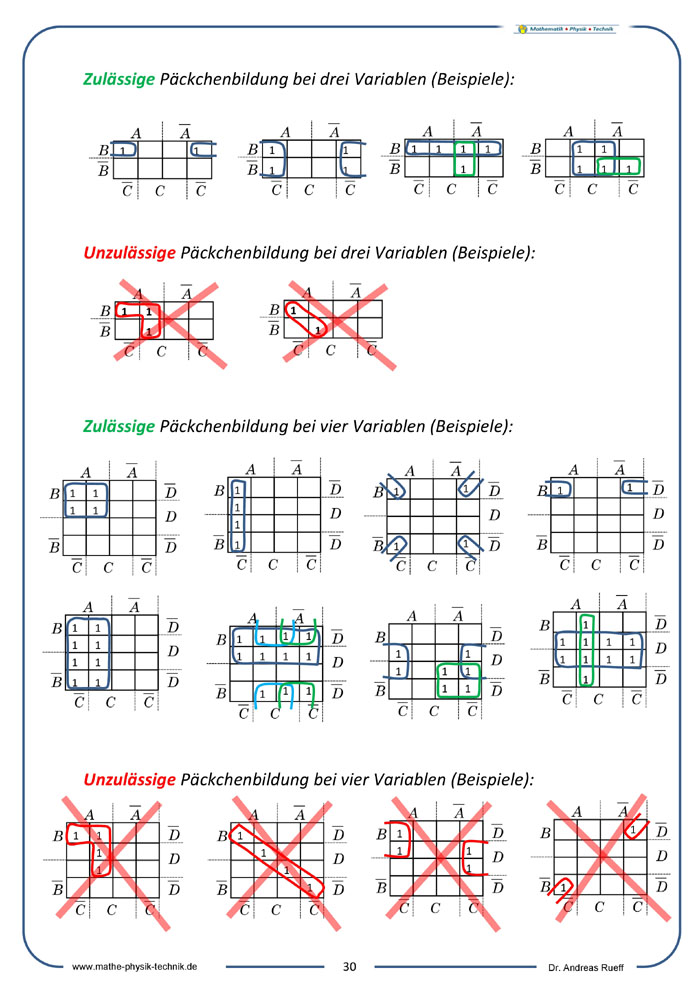
Vereinfachung der ODER-Normalform: KV-Diagramme
SCHALTUNGSSYNTHESE (AUFGABEN - 1)
SCHALTUNGSSYNTHESE (AUFGABEN - 2)
DATEN SPEICHERN
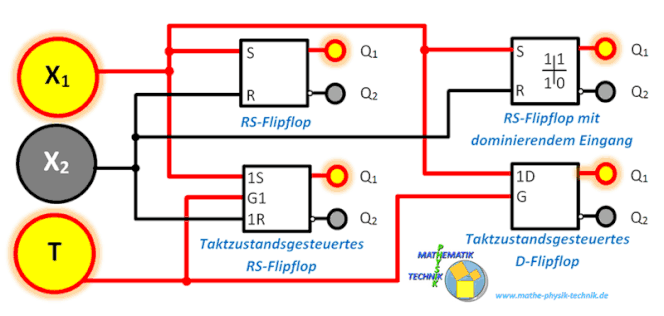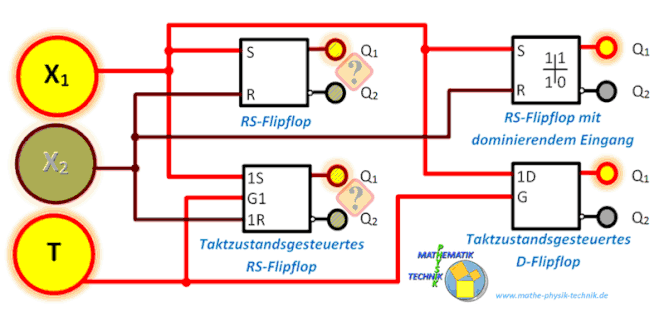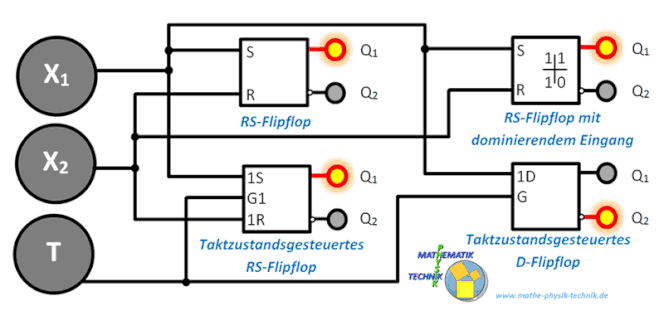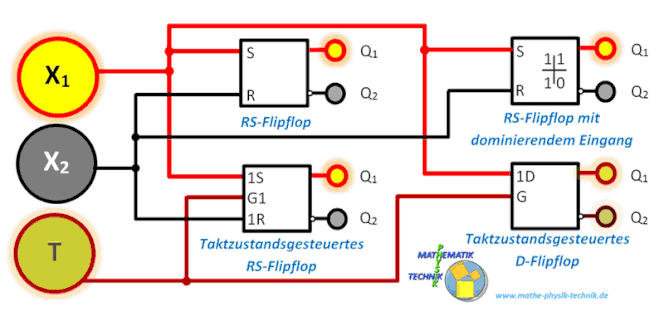
Das Flipflop
Funktionsweise – RS-Flipflop
Aufbau eines RS-Flipflops durch NAND-Glieder
RS-Flipflop mit dominierendem Eingang
Taktzustandsgesteuertes RS-Flipflop (Auffang-Flipflop)
D-Flipflop
Taktflankengesteuerte Flipflops
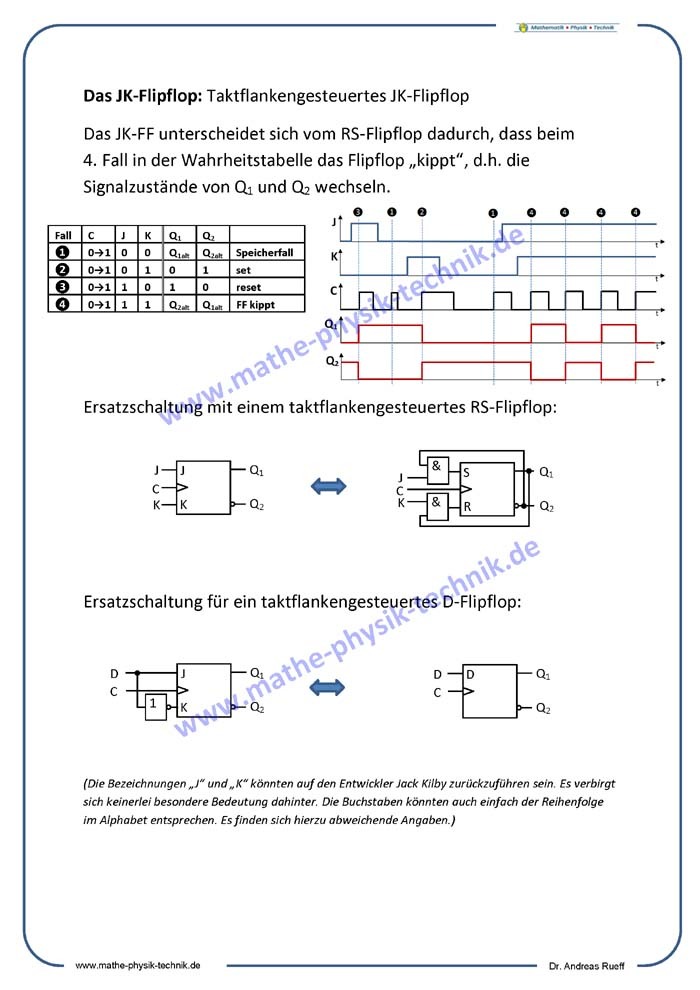
Taktflankengesteuertes RS-Flipflop
Taktflankengesteuertes D-Flipflop
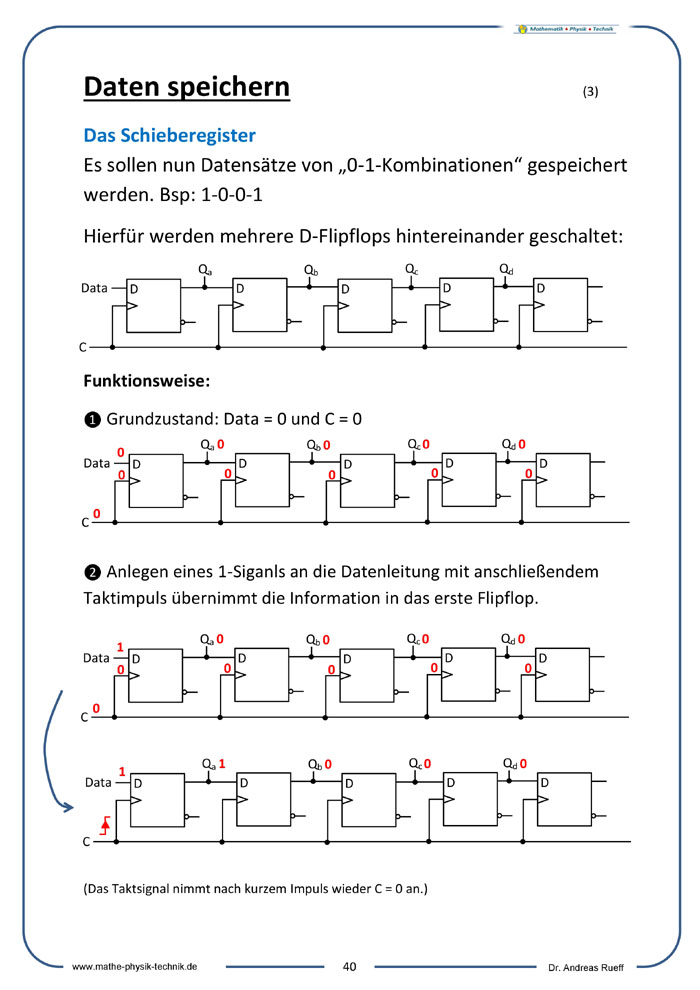
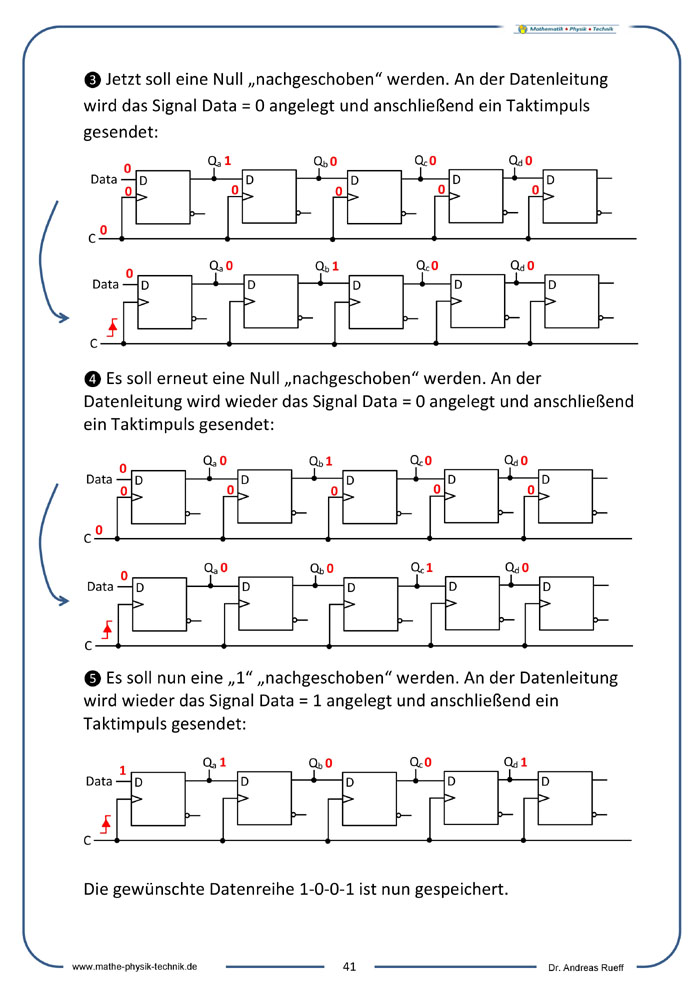
Das Schieberegister
RECHENSCHALTUNGEN
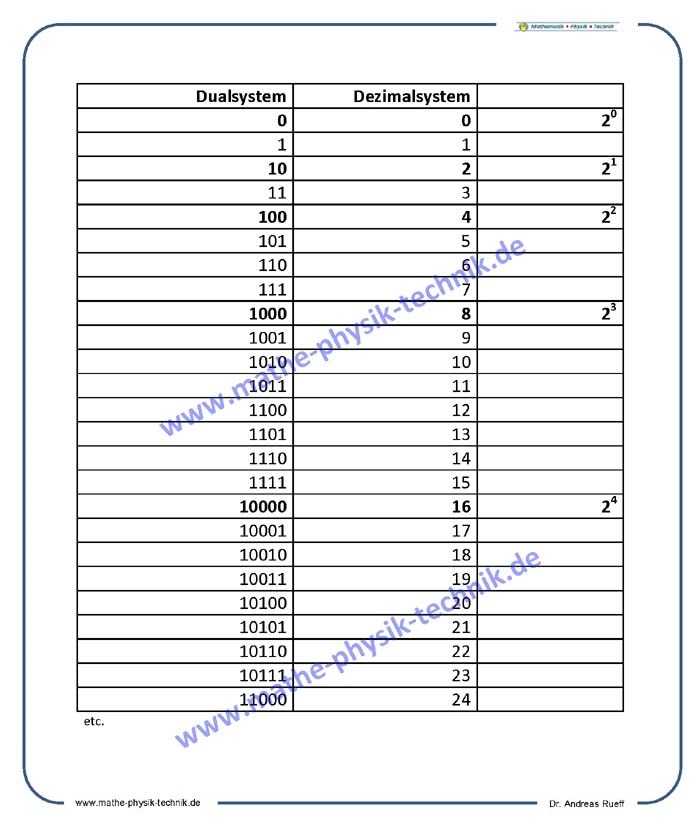
Dualzahlen
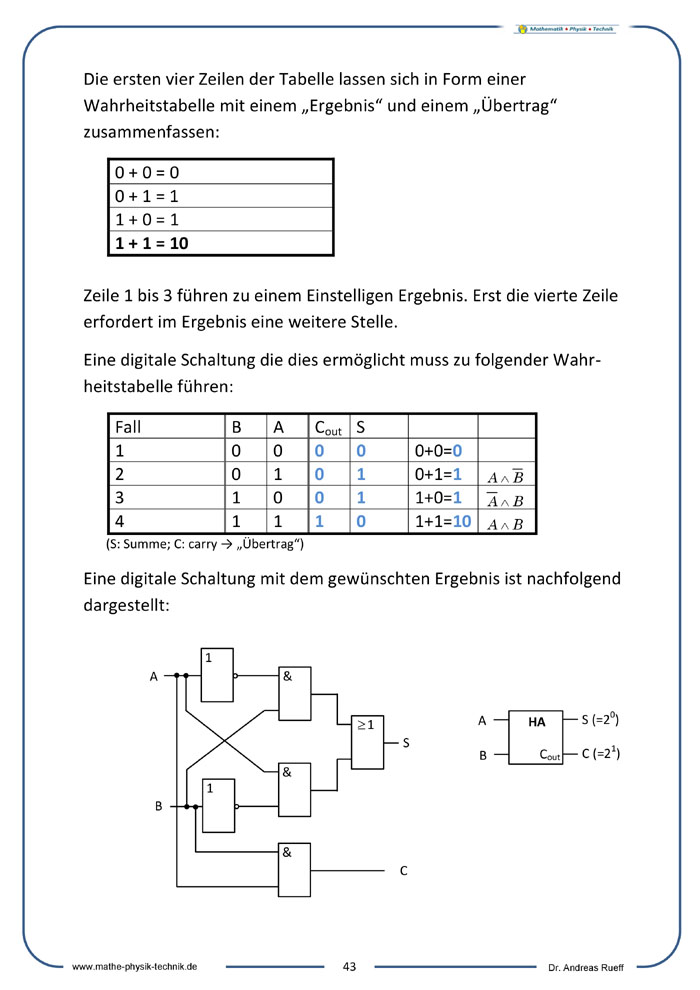
Der Halbaddierer
Der Volladdierer (FA – engl. full adder)
Die Paralleladdierschaltung
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen
Hinweis:
Für die Unterrichtseinheit ist die Anschaffung des Skripts für meine Schüler*innen nicht notwendig! Die Folien werden nacheinander bearbeitet und notwendige Materialien ggf.
kopiert.
Skripte:
Boolesche Algebra
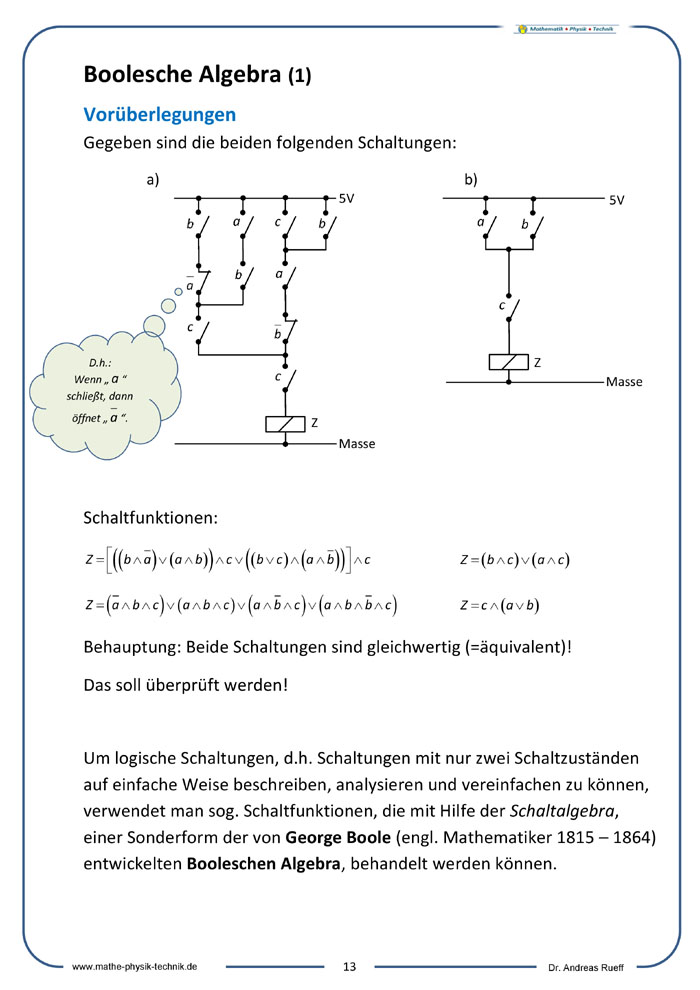
George Boole und die boolesche Algebra
George Boole (* 2. November 1815 in Lincoln, England; † 8. Dezember 1864 in Ballintemple, in der Grafschaft Cork, Irland) war ein englischer Mathematiker, Logiker und Philosoph. George Boole
war zudem Autodidakt, das ist ein Mensch, der sich selbstständig Wissen oder Fertigkeiten aneignet beziehungsweise durch Beobachtung, Versuche, Übung, Videos oder Lektüre
eigenständig erworben hat.
Er ist vor allem dadurch bekannt, dass die für die Computertechnik
grundlegende boolesche Algebra nach ihm benannt wurde. Boole erkannte als erster, dass die Aussagenlogik als eine Algebra aufgefasst werden kann, die zwei Elemente hat (heute
als die zwei Wahrheitswerte „0“ und „1“ bezeichnet). Unter „Algebra“ versteht man ganz allgemein eigentlich eines der grundlegenden Teilgebiete der Mathematik; es befasst sich mit den
Eigenschaften von Rechenoperationen (z.B. die Grundrechenarten: addieren, subtrahieren, dividieren und multiplizieren). Im Volksmund wird Algebra häufig als das „Rechnen mit
Unbekannten (Variablen) in Gleichungen“ bezeichnet.
Die Arbeiten von George Boole markieren den Beginn einer Entwicklung, mit der die Logik in die Mathematik integriert wurde.
Leben
George Boole wurde in Lincolnshire geboren. Er hatte außer der Grundschulbildung keine weiterführenden Schulen besucht. Er brachte sich autodidaktisch Altgriechisch, Französisch und Deutsch
bei. Mit 16 Jahren wurde er Hilfslehrer, um seine Familie finanziell zu unterstützen. Im Alter von 19 Jahren gründete Boole seine eigene Schule. Auf Grund seiner
wissenschaftlichen Arbeiten wurde er 1848 Mathematikprofessor am Queens College in Cork (Irland), obwohl er selbst keine Universität besucht hatte. Dort lernte er Mary
Everest kennen, seine spätere Frau. Sie war mathematisch interessiert, arbeitete als Bibliothekarin und setzte sich mit der Didaktik der Mathematik auseinander. Ihr Onkel
George Everest war Namensgeber des höchsten Bergs der Welt. Von der Royal Society (nationale Akademie der Wissenschaften des Vereinigten Königreiches für die
Naturwissenschaften) wurde Boole 1844 mit der Royal Medal (Auszeichnung für Wissenschaftler, die besonders wichtige Beiträge zur Weiterentwicklung der Wissenschaften
geleistet haben) ausgezeichnet. 1847 publizierte er sein epochemachendes Logikwerk The Mathematical Analysis of Logic und begründete damit die
moderne mathematische Logik. Als Verallgemeinerungen von Booles Arbeiten wurde später die sogenannte boolesche Algebra nach ihm benannt. 1854 veröffentlichte er dann sein ausführlicheres Buch
An Investigation of the Laws of Thought. 1857 wurde er zum Mitglied der Royal Society gewählt. George Boole starb am 8. Dezember 1864 mit nur 49 Jahren an einer
fiebrigen Erkältung. Auf seinem Fußweg ging er zwei Meilen weit im strömenden Regen zur Universität, wo er anschließend seine Vorlesung in durchnässten Kleidern hielt. Er erkältete sich,
bekam hohes Fieber und erholte sich davon später nicht mehr.
1964 wurde der Mondkrater Boole nach ihm benannt, ebenso 2001 der Asteroid (17734) Boole.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
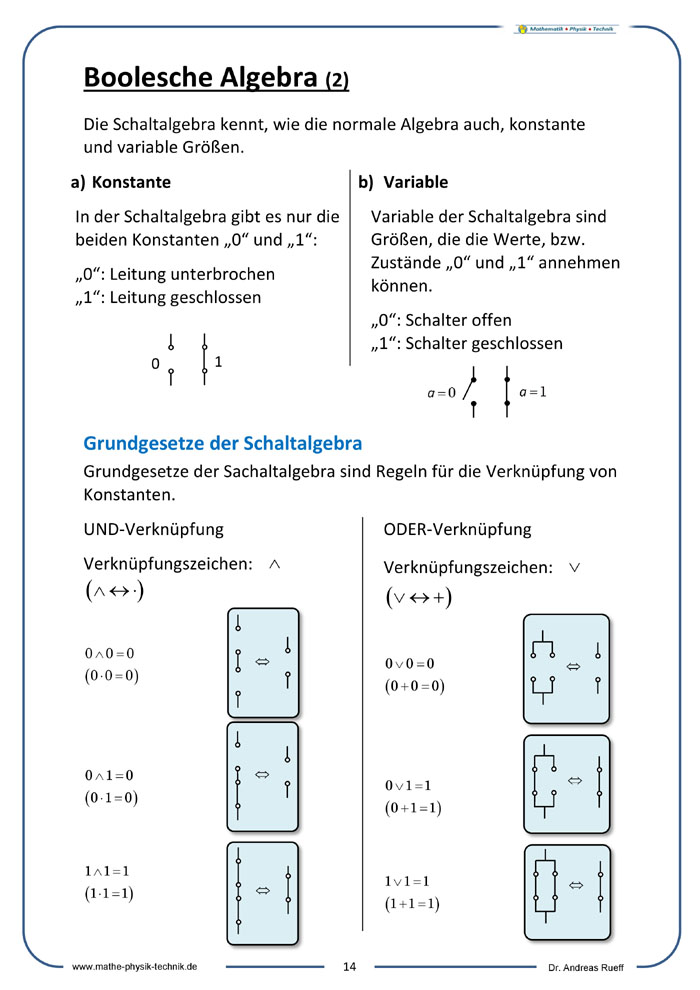
Augustus De Morgan
Augustus De Morgan (* 27. Juni 1806 in Madurai, Indien; † 18. März 1871 in London) war ein englischer Mathematiker. Er war Mitbegründer und erster Präsident der London Mathematical
Society.
Augustus De Morgan wurde als Sohn eines in Indien stationierten Soldaten geboren, seine Familie kehrte aber bald nach England zurück. Er fiel in der Schule kaum auf, interessierte sich jedoch
von jeher für merkwürdige Zahlenspiele. 1823 besuchte er das Trinity College in Cambridge. Das Trinity College ist ein College der University of Cambridge und beheimatet ungefähr 1000
Studenten und rund 190 Lehrpersonen. Es besitzt eine starke akademische Tradition und hat bisher 34 Nobelpreisträger sowie vier Träger der Fields-Medaille hervorgebracht. De Morgan kehrte
1826 nach London zurück und erhielt dort 1828 am neu gegründeten University College einen Lehrstuhl.
De Morgan war ein Freund von Charles Babbage. Babbage ist vor allem für die von ihm entwickelte Rechenmaschine Analytical Engine bekannt. Diese gilt als Vorläufer des modernen Computers. De
Morgan verfasste zahlreiche mathematische Artikel wie Elements of Arithmetic (1830 und Formal Logic (1847), eine seiner wichtigsten Arbeiten. 1838 verwendete er als erster den Begriff
„mathematische Induktion“, ein wichtiges mathematisches Beweisverfahren.
Am bekanntesten wurde er durch zwei nach ihm benannte Regeln, die Morganschen Gesetze (auch: „De Morgansche Gesetze“). Diese
besagen, dass jede UND-Verknüpfung durch eine ODER-Verknüpfung ausgedrückt werden kann und umgekehrt. Sie wurden seither häufig bei mathematischen Beweisen und auch bei der Programmierung
verwendet. Die Morganschen Gesetze haben wichtige Anwendungen in der Elektrotechnik, der Physik und der Informatik. Insbesondere werden die Morganschen Gesetze beim Entwurf von digitalen
Schaltungen genutzt, um die Typen der verwendeten logischen Schaltelemente gegeneinander auszutauschen oder Bauteile einzusparen. De Morgan gilt heute gemeinsam mit George Boole als Begründer
der formalen Logik.
De Morgan war von 1865 bis 1866 der erste Präsident der London Mathematical Society, sie ist die führende Mathematikervereinigung in England.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Hinweis: Die erste Karte ist mit dem kleinen "i" gekennzeichnet, ziehe sie an die oberste Stelle. Aus der Aufgabenstellung kannst du auch die letzte Karte entnehmen.
Bringe dann die übrigen Karten in die richtige Reihenfolge.
(Empfehlung: Arbeite im Vollbildmodus - Klicke auf das Symbol oben rechts in der Onlineübung)
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Schaltungssynthese (KV-Diagramme)
Diese App wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
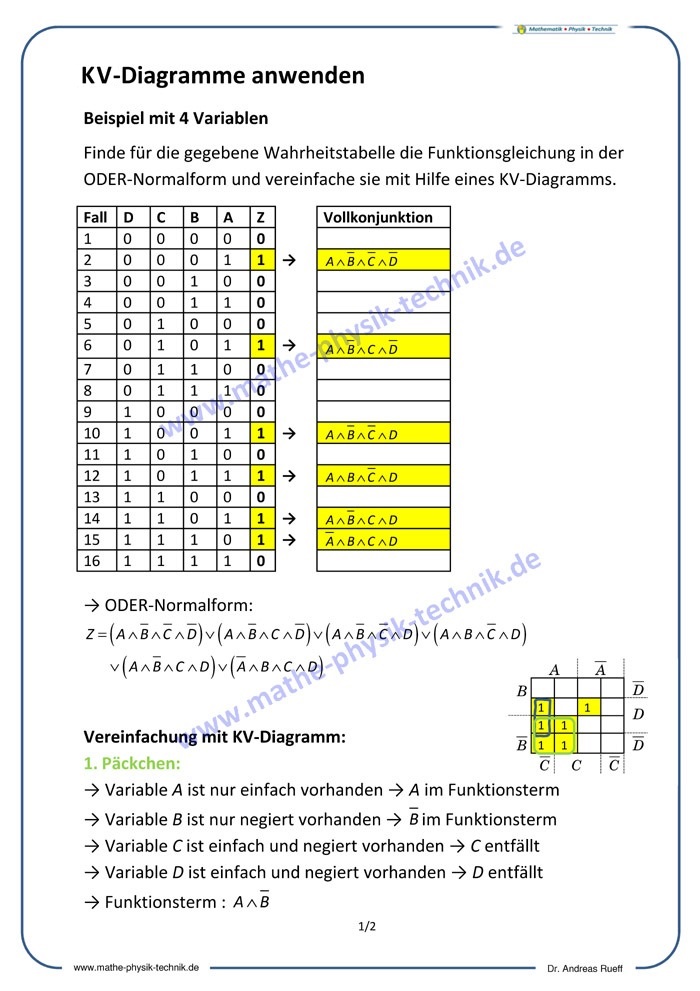
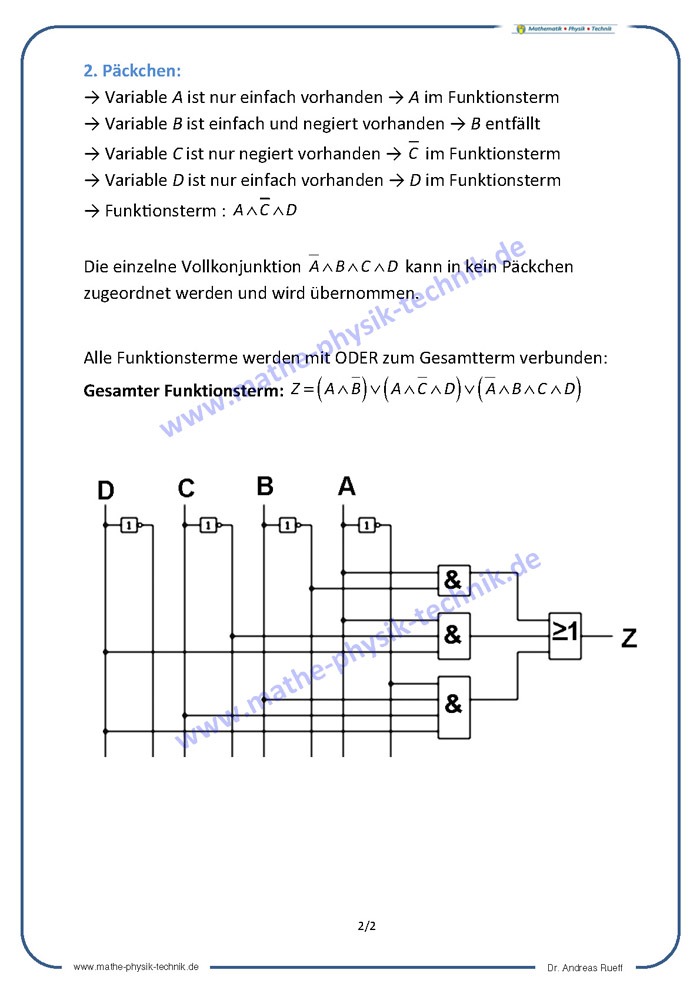
Daten speichern (Flipflops, Schieberegister)
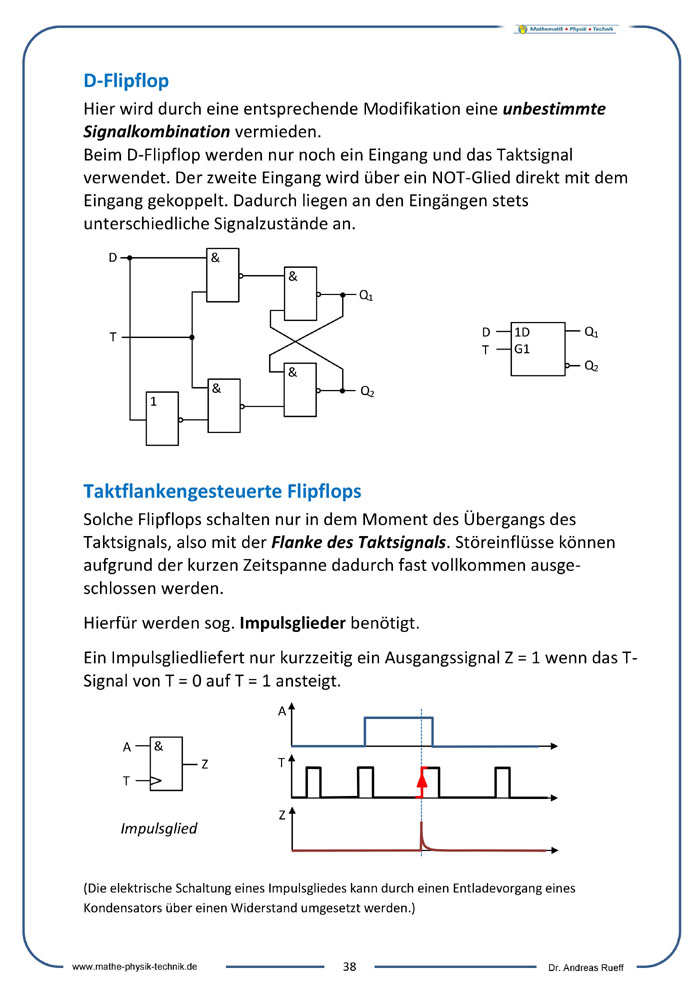
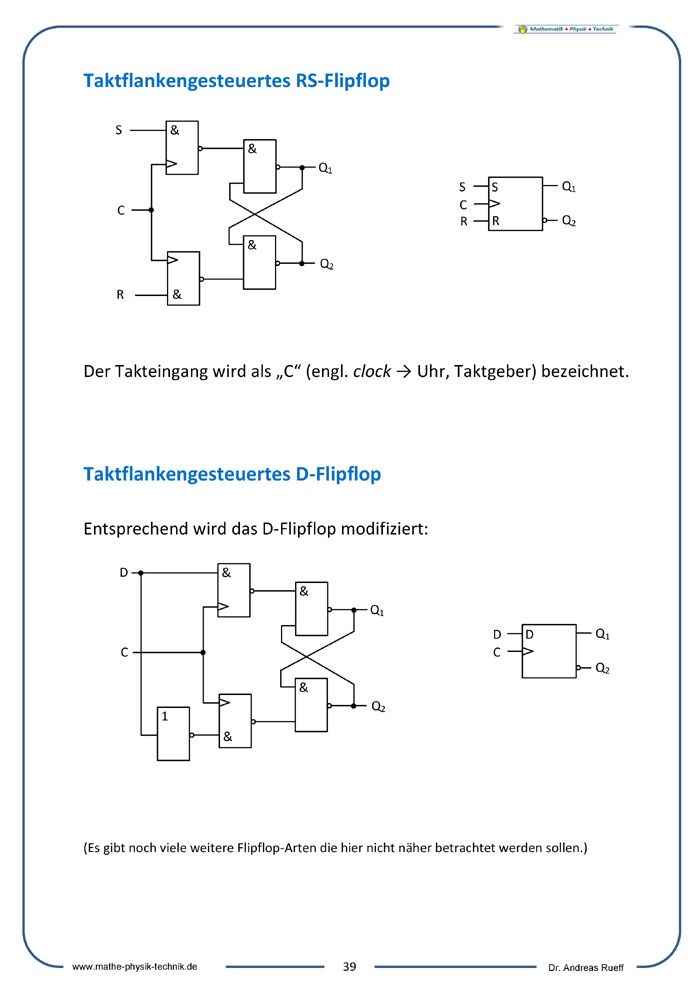
Rechenschaltungen (Halb- und Volladdierer)
Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hier einige Links die dich auch interessieren könnten:
Das Wissenschaftsjahr 2014 widmet sich der digitalen Revolution und ihren Folgen für unsere Gesellschaft. Wie verändern die digitalen Technologien unseren Alltag? Wie sieht die Zukunft unserer Kommunikation, Industrie und Arbeitswelt aus? Hier erfahren Sie mehr über die Hintergründe und Initiatoren des Jahres.
Das Bundesamt für Sicherheit in der Informationstechnik (BSI)
Wie mache ich meinen PC sicher? Welche Gefahren begegnen mir im Netz? Wie bewege ich mich sicher im Internet und im mobilen Netz? Das Bundesamt für Sicherheit in der Informationstechnik (BSI) ist der zentrale IT-Sicherheitsdienstleister des Bundes. Das BSI trägt dazu bei, die IT-Sicherheit in Deutschland zu erhöhen.
Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hinweis: Es werden keine Bücher oder sonstige, hier benannte Materialien im Unterricht verwendet oder benötigt.
Quellenangaben zu den Inhalten auf dieser Seite
Infotext [13] - George Boole und die boolesche Algebra
Dieser Text basiert auf den Artikeln George Boole, Autodidakt, Algebra, Royal Society
und Royal Medal aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der
Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist
eine Liste der Autoren verfügbar.
Die Abbildung wurde aus Wikimedia Commons entnommen: Datei: George Boole color.jpg
Infotext [16] - August De Morgan
Dieser Text basiert auf den Artikeln Augustus De Morgan , De-morgansche_Gesetze , London Mathematical Society ,
Trinity College (Cambridge) und Charles Babbage aus der
freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA
3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Hintergrundbild: Erstellt von A. Rueff unter Verwendung der folgenden Vorlage von Pixabay: Bild von Gerd Altmann auf Pixabay