
Analysis (1)
Auf dieser Seite findest du die Folien zur Unterrichtseinheit ANALYSIS
Inhalt - Analysis
Teil 1:
Folgen und Reihen
Grenzwerte von Funktionen
Nullstellen von Polynomfunktionen
Lösungsmethoden für Polynomfunktionen
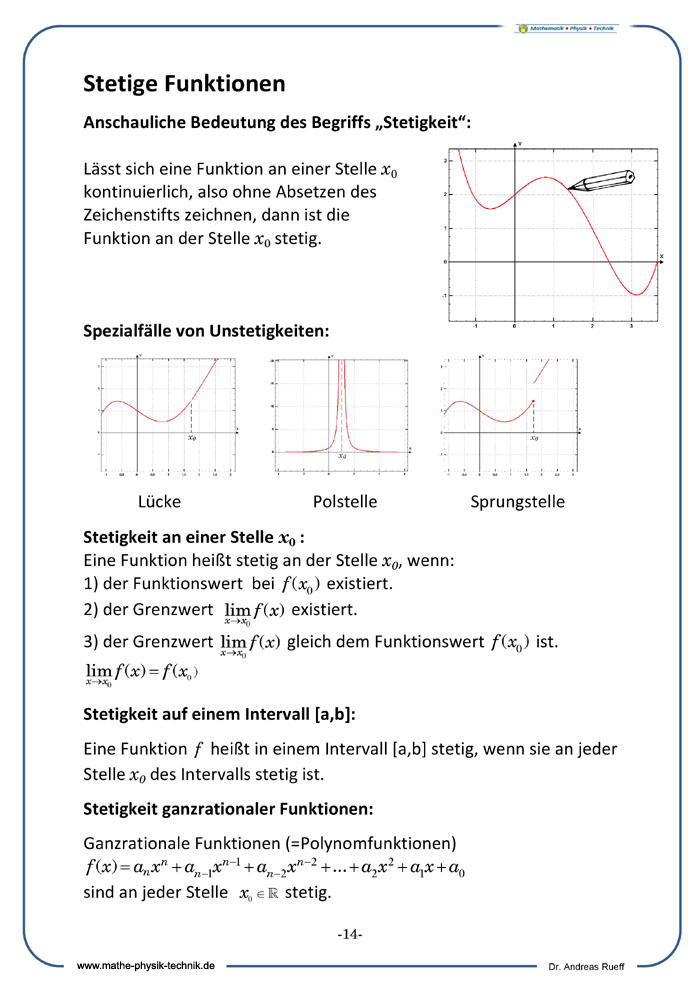
Stetige Funktionen
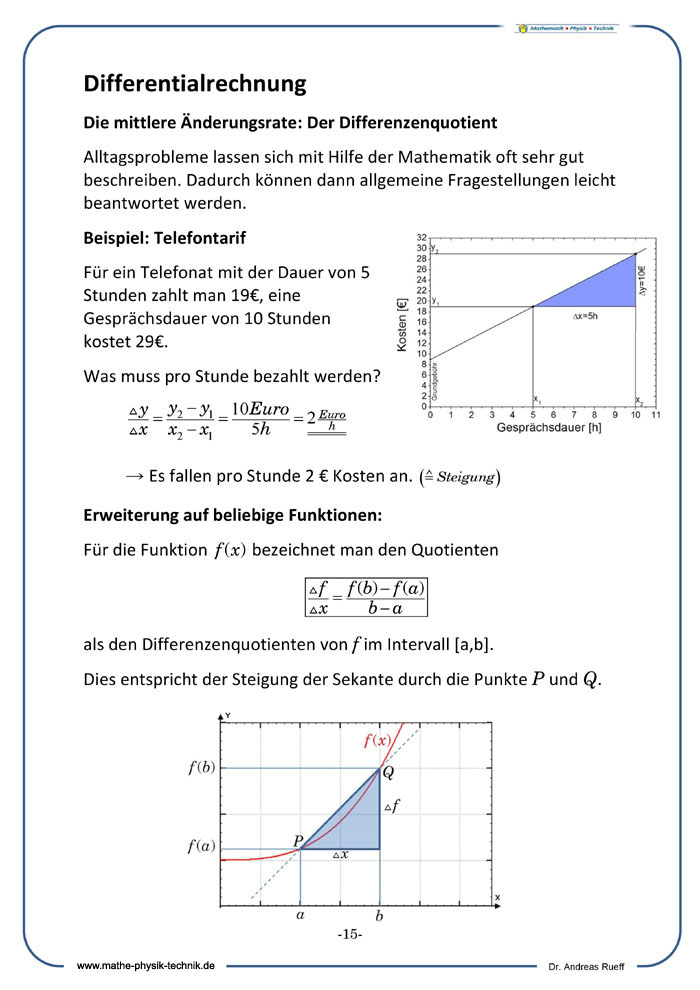
Differentialrechnung
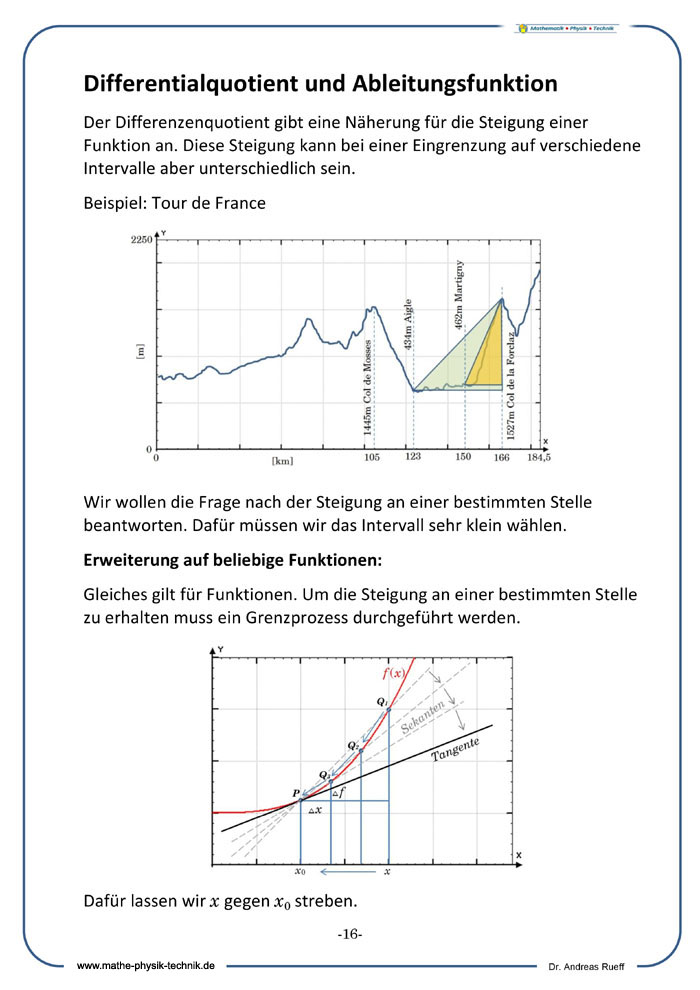
Differentialquotient und Ableitungsfunktion
Rechnerische Bestimmung der Ableitungsfunktion
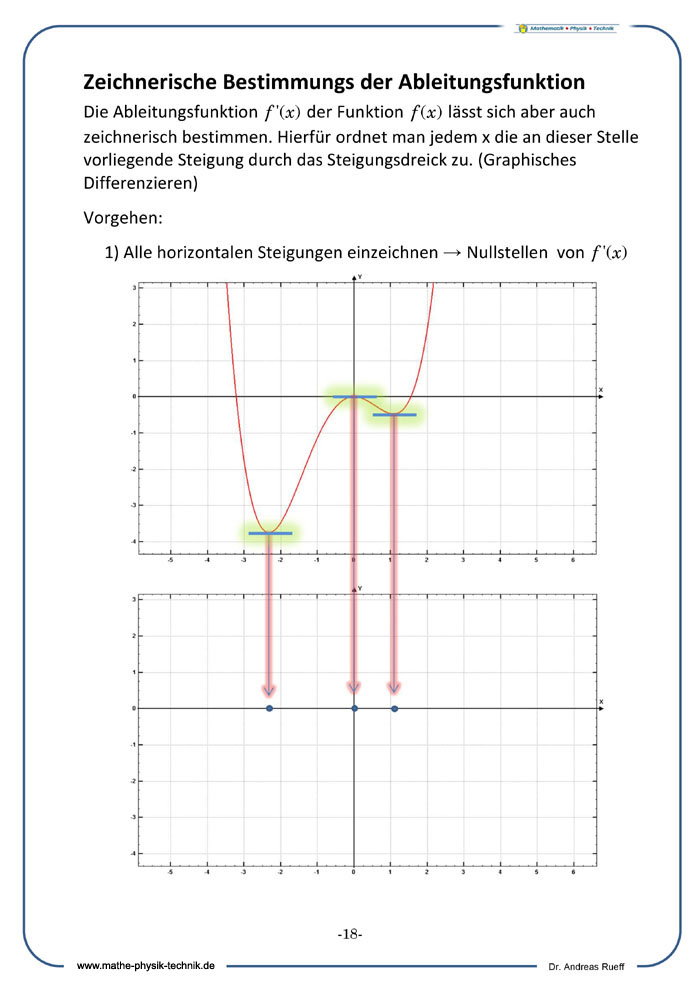
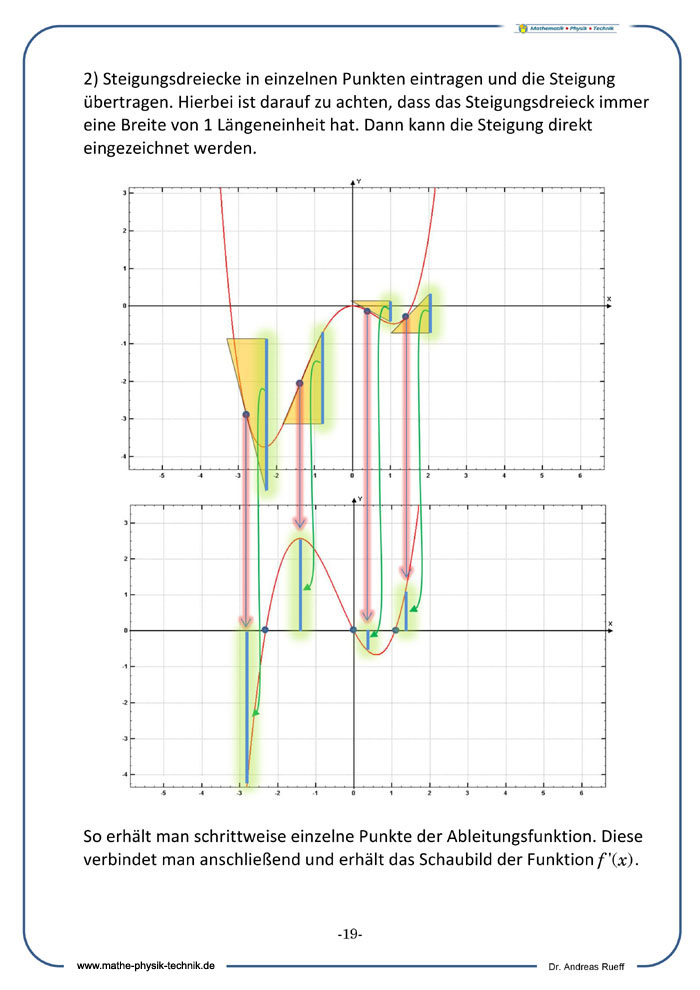
Zeichnerische Bestimmung der Ableitungsfunktion
Exponentialfunktionen ableiten
Ableitungsregeln
Die Produktregel (Herleitung)
Die Quotientenregel (Herleitung über die Produktregel)
Die Kettenregel (Herleitung)
Kurvenuntersuchungen
Monotonieverhalten
Monotoniekriterium für differenzierbare Funktionen
Krümmung der Funktion
Extrema und Wendepunkte
Kurvendiskussion ganzrationaler Funktionen
Beispiel: Kurvenuntersuchung
Anwendungen (1) Tangentenproblem
Anwendungen (2) Steigungswinkel
Anwendungsbeispiel: Senkrechter Wurf
Anwendungsbeispiel: Bierdosen-Mathematik
Integralrechnung - Streifenmethode
Die Flächeninhaltsfunktion
Das unbestimmte und das bestimmte Integral
Rechenregeln für unbestimmte Integrale
Das bestimmte Integral
Rechenregeln für unbestimmte Integrale:
Übung: Berechne die unbestimmten Integrale
Übung: Das bestimmte Integral - Flächenberechnungen
Rotationskörper
Beispielaufgaben - Rotationskörper
Die Eulersche Zahl e
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen



Analysis: Folgen und Reihen - Gaußsche Summenformel:
Analysis - Veranschaulichung der Summenformel [3:58]
Die Gaußsche Summenformel wird anhand eines Beispiels erklärt und anschließend verallgemeinert.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)




Diese App ist eingebunden unter Verwendung von Geogebra [GNU General Public License (version 3 or later)].

Diese App ist wurde erstellt von frauschulze bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von Christian Kratochwil bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von M. Breede bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von bos2019 bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App ist wurde erstellt von Simon Oswald bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
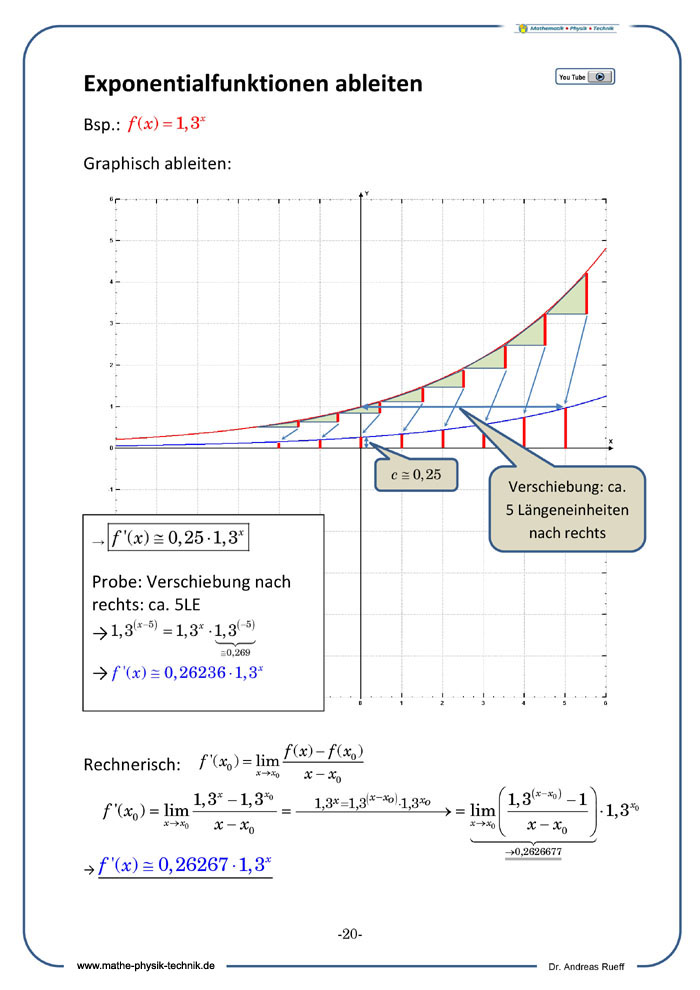

Analysis: Exponentialfunktionen ableiten (1): [6:36]
Graphisches Ableitungsverfahren
Mathematik - Analysis: Es wird die Ableitung von Exponentialfunktionen am Beispiel von f(x)=2^x graphisch vorgeführt. Im zweiten Teil wird das rechnerische Differenzieren (mit Differentialquotient) gezeigt.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Analysis: Exponentialfunktionen ableiten (2): [3:23]
Rechnerisches Ableitungsverfahren
Mathematik - Analysis: Es wird die Ableitung von Exponentialfunktionen am Beispiel von f(x)=2^x rechnerisch vorgeführt. Im ersten Teil wird das graphische Ableitungsverfahren zu dieser Funktion gezeigt.
![[Bild kann nicht geladen werden]](https://dl.dropbox.com/s/p18kegowcw9fjq6/Trennlinie%201%20animiert.gif?dl=0)

Diese App ist wurde erstellt von Dr. Christina Bauer bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!



Erfahrungsbericht zu den Materialien:
Als geeignete Materialien haben sich u. a. die folgenden Taschenrechner erwiesen:
1) Für die Mittelstufe vollkommen ausreichend und weniger kompliziert in der
Handhabung: TI-30
2) Für die Oberstufe mit allen notwendigen Funktionen: Casio FX-991DE Plus (Dieser TR kann beispielsweise auch Integralrechnung, Vektorrechnung, Gleichungssysteme lösen, Statistik u.v.m.)
Using PhET Simulations in Teaching
-
Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).





























