Mathematik - Grundlagen für die Mittelstufe

Zahlensysteme (ℕ, ℚ, ℝ) [1/7] Gleichungen und Ungleichungen [2/7] Gleichungssysteme [3/7] Proportionen und Anwendungen [4/7] Funktionen [5/7] Geometrie [6/7] Statistik & Wahrscheinlichkeit [7/7] Fit für die Oberstufe Regelheft Analysis Analytische Geometrie Stochastik Tools

Stochastik (1)

Auf dieser Seite findest du die Folien zur Unterrichtseinheit STOCHASTIK

Inhalt - Stochastik

Teil 1:

Einteilung
Begriffe
Spezialfälle
Häufigkeit und Wahrscheinlichkeit
Empirisches Gesetz der großen Zahl (Bernoulli)
Wahrscheinlichkeitsverteilung
Summenregel
Gegenwahrscheinlichkeit
Additionssatz
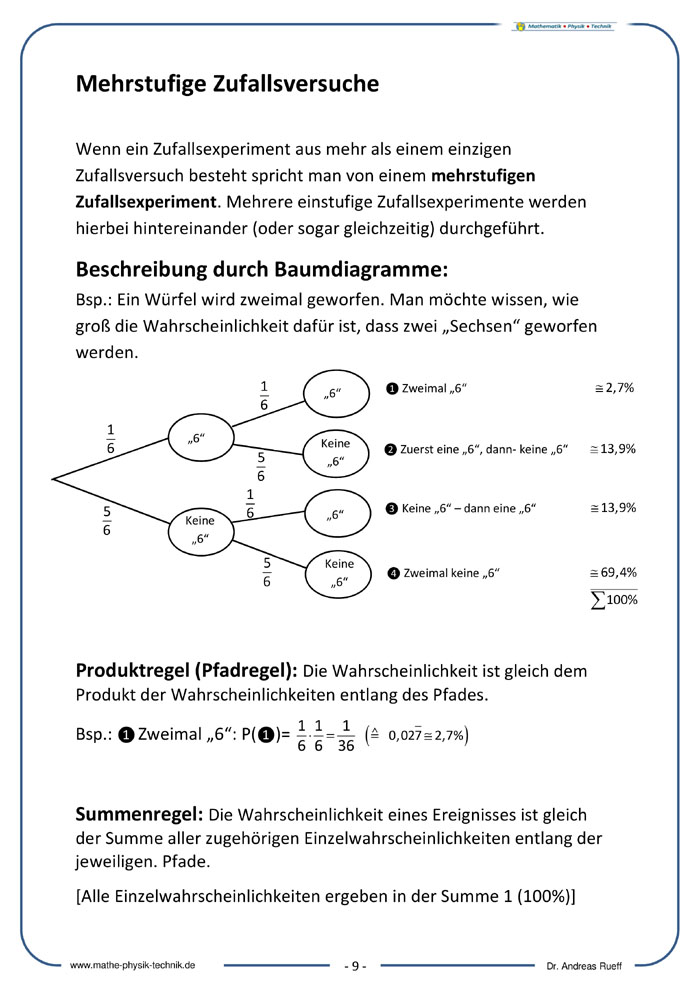
Mehrstufige Zufallsversuche
Beschreibung durch Baumdiagramme
Produktregel (Pfadregel)
Summenregel
Kombinatorik
① Permutationen
② Variationen
③ Kombinationen
Erläuterung zur Formel [③-❷]
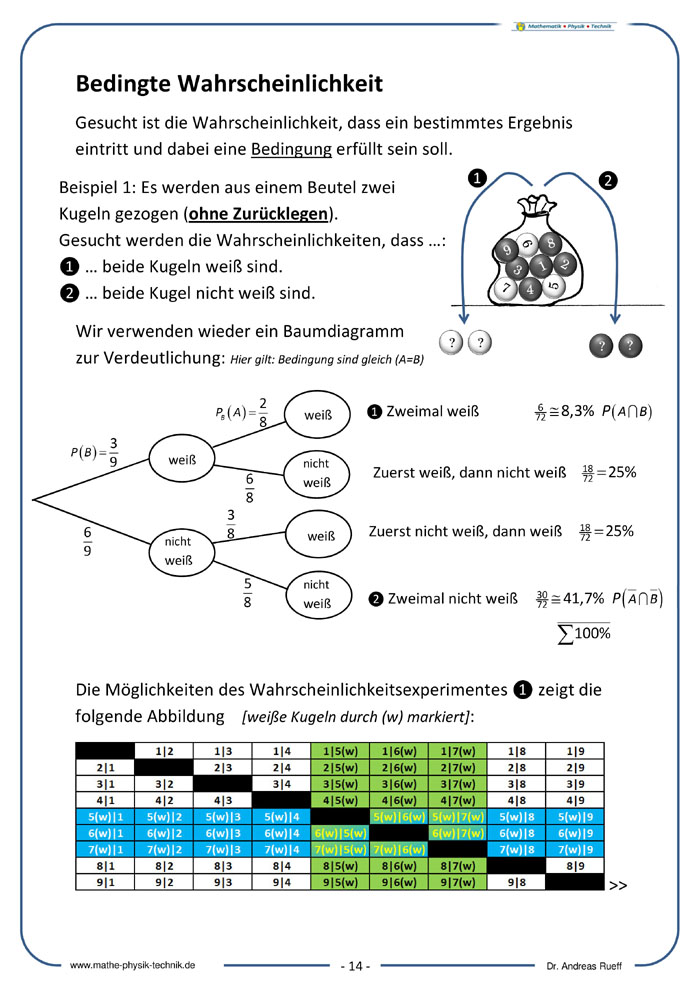
Bedingte Wahrscheinlichkeit
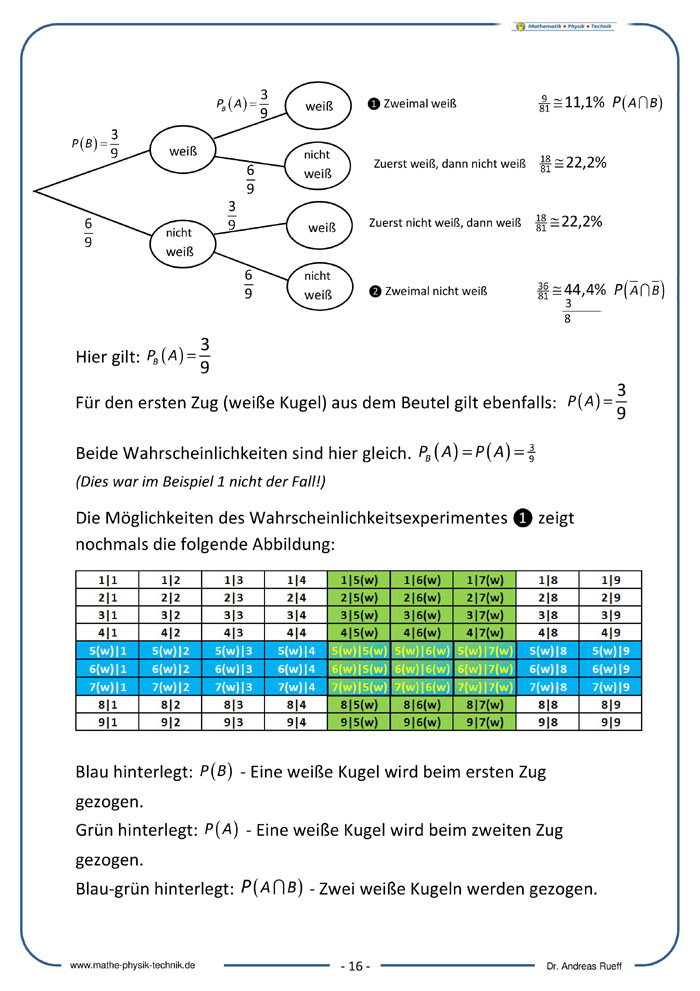
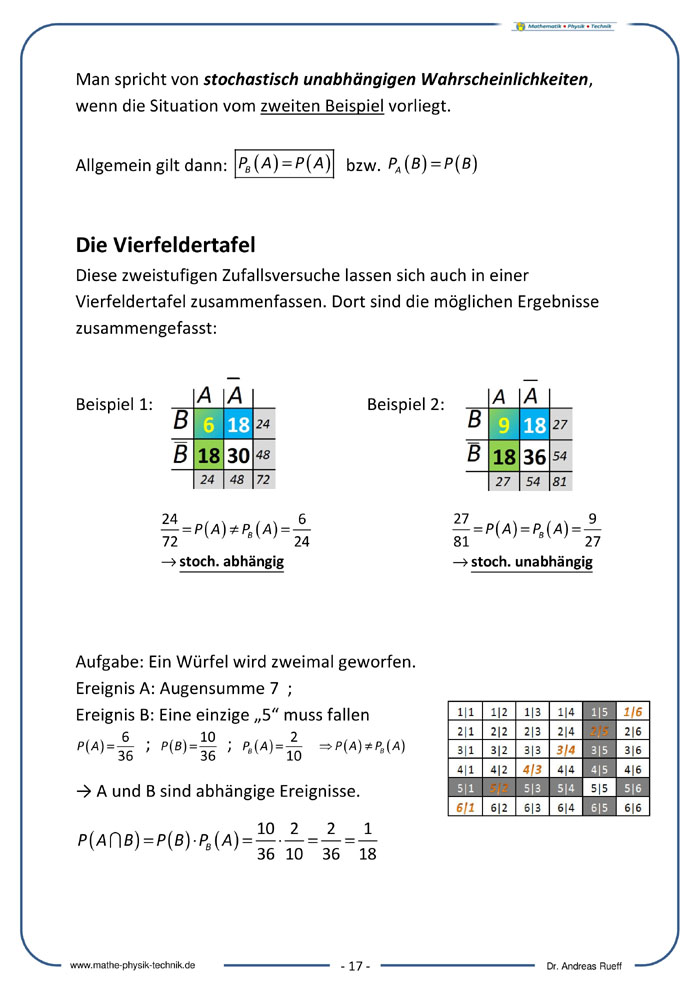
Abhängige und Unabhängige Ereignisse
Die Vierfeldertafel
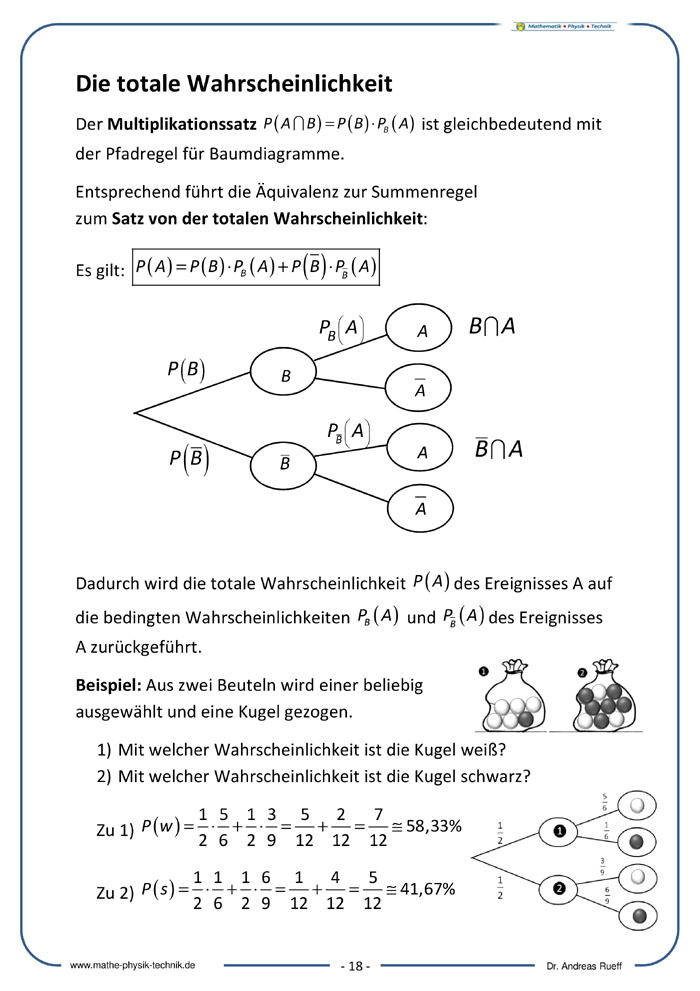
Die totale Wahrscheinlichkeit
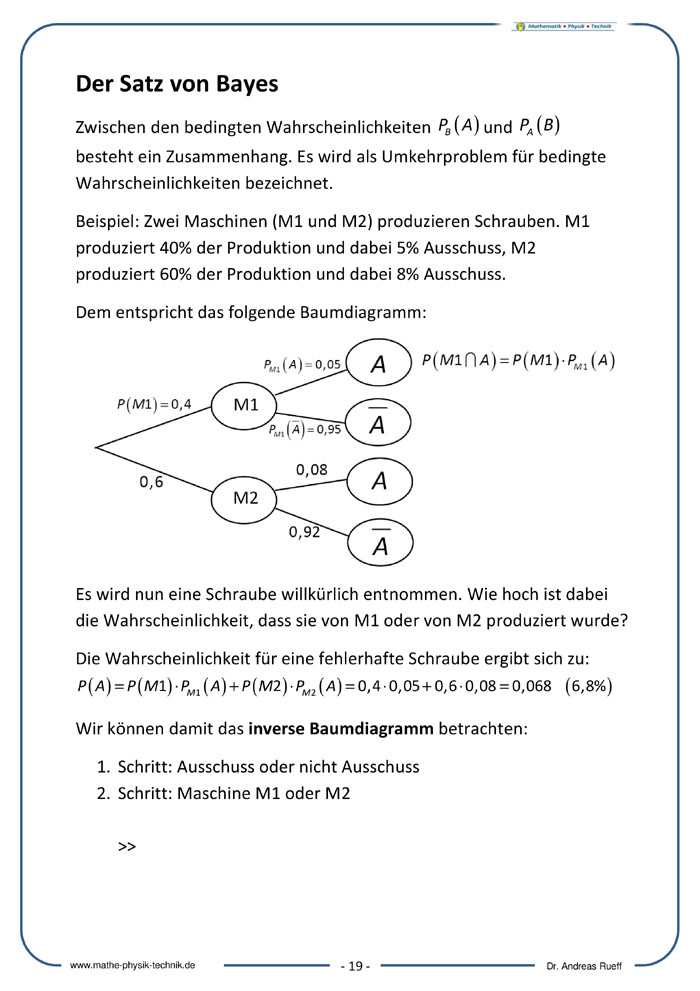
Der Satz von Bayes
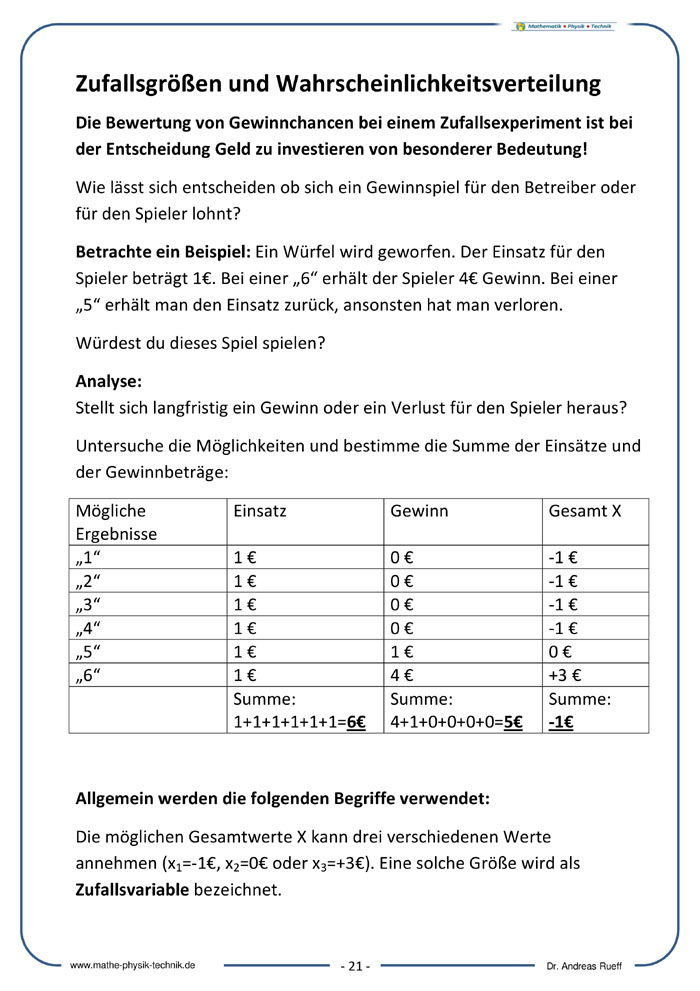
Zufallsgrößen und Wahrscheinlichkeitsverteilung
Der Erwartungswert
Standardabweichung und Varianz
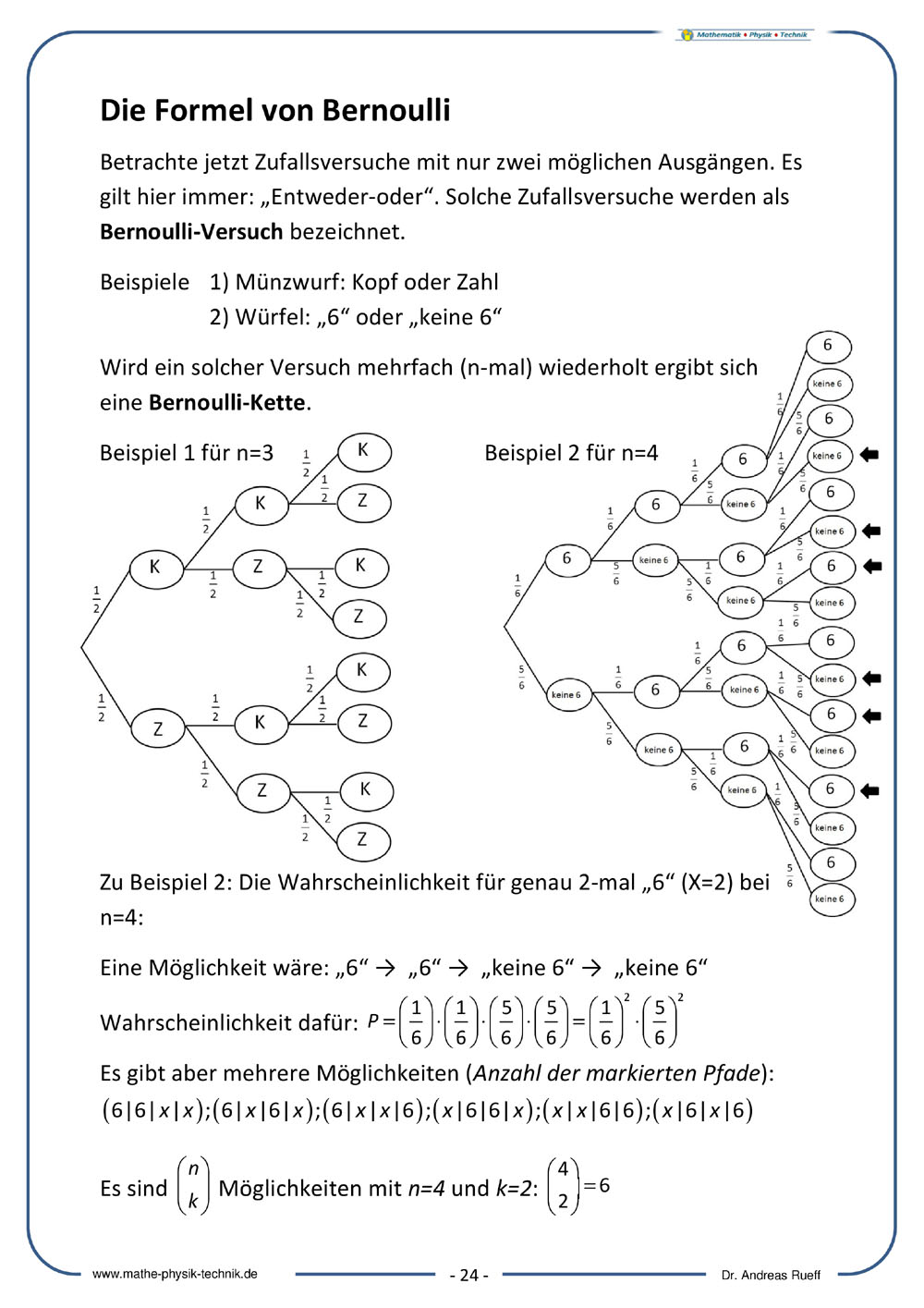
Die Formel von Bernoulli

→ Teil 2:

Die Binomialverteilung
Systematische Untersuchung der Binomialverteilung:
Systematische Anwendung der Binomialverteilung
Die kumulierte Binomialverteilung
Der Erwartungswert bei Bernoulli-Ketten
Die Standardabweichung bei Bernoulli-Ketten
Die Normalverteilung
Globale Näherungsformel von Laplace und de Moivre
Anhang: Tabellen

Allgemeine Hinweise zu den Themenseiten

Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.

Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.

Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.

Siehe hierzu auch: → Konzept - mathe-physik-technik.de

Skript → Publikationen

Hinweis:
Für die Unterrichtseinheit ist die Anschaffung des Skripts für meine Schüler*innen nicht notwendig! Die Folien werden nacheinander bearbeitet und notwendige Materialien ggf. kopiert.

Skripte

→ Publikationen

Diese App ist wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Hinweise und Anregungen zur Aktualisierung dieser Seite oder zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Diese App ist wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Hinweise und Anregungen zur Aktualisierung dieser Seite oder zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Kombinatorik

Der Begriff leitet sich ab von lateinisch combinatio ‚Zusammenfassung‘. Historisch entstand die Kombinatorik aus Abzählproblemen von diskreten (abzählbaren) Strukturen, wie sie im 17. Jahrhundert bei der Wahrscheinlichkeitsanalyse von Glücksspielen auftraten. Dieser klassische Bereich der Kombinatorik wird zusammenfassend als abzählende Kombinatorik (Stichwörter: Permutationen, Variationen und Kombinationen) bezeichnet.

Permutationen: Unter einer Permutation (von lateinisch permutare ‚vertauschen‘) versteht man in der Kombinatorik eine Anordnung von Objekten in einer bestimmten Reihenfolge. Je nachdem, ob manche Objekte mehrfach auftreten dürfen oder nicht, spricht man von einer Permutation mit Wiederholung oder einer Permutation ohne Wiederholung.

-----------------------------------

Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Diese App ist wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Hinweise und Anregungen zur Aktualisierung dieser Seite oder zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Aufgaben: Permutationen

In einer Urne befinden sich 8 durchnummerierte Kugeln, sie tragen die Zahlen 1 bis 8. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 6 durchnummerierte Kugeln, sie tragen die Zahlen 4 bis 9. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 5 Kugeln mit den Zahlen 1, 1, 2, 3, 4. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 6 Kugeln mit den Zahlen 1, 2, 2, 3, 3, 4. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 7 Kugeln mit den Zahlen 1, 1, 2, 3, 4, 4, 5. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 8 Kugeln mit den Zahlen 1, 2, 2, 2, 3, 4, 5, 6. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 6 Kugeln mit den Zahlen 2, 2, 3, 3, 4, 5. Wie viele verschiedene Permutationen gibt es?
In einer Urne befinden sich 9 Kugeln mit den Zahlen 1, 1, 1, 2, 3, 4, 5, 6, 7. Wie viele verschiedene Permutationen gibt es?

Binomialkoeffizienten, Binome und Pascalsches Dreieck

Binomialkoeffizienten

Diese App ist wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Hinweise und Anregungen zur Aktualisierung dieser Seite oder zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Aufgaben: Variationen (Reihenfolgen)

In einer Urne befinden sich 15 durchnummerierte Kugeln (1 bis 15). Es werden 6 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 20 durchnummerierte Kugeln (1 bis 20). Es werden 4 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 10 durchnummerierte Kugeln (1 bis 10). Es werden 3 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 12 durchnummerierte Kugeln (1 bis 12). Es werden 4 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
Aus einem Skat-Kartenspiel (32 Karten) werden die Kreuzkarten herausgenommen. Es werden 3 Karten aus den verbleibenden 24 Karten gezogen, ohne Zurücklegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es für diese Karten?
In einer Urne befinden sich 8 durchnummerierte Kugeln (1 bis 8). Es werden 5 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 18 durchnummerierte Kugeln (1 bis 18). Es werden 6 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es, die bei dieser Ziehung möglich sind?
Aus einem Skat-Kartenspiel (32 Karten) werden die Karo-Karten herausgenommen. Es werden 4 Karten aus den verbleibenden 24 Karten gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen (Variationen) gibt es für diese Karten?

Aufgaben: Kombinationen

1. In einer Urne befinden sich 15 durchnummerierte Kugeln (1 bis 15). Es werden 6 Kugeln gezogen, ohne diese zurückzulegen. Wie viele Möglichkeiten gibt es, diese 6 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?

2. Mengen und Teilmengen: Wie viele 5-elementige Teilmengen hat eine 25-elementige Menge? (Alternative Formulierung: In einer Urne befinden sich 25 durchnummerierte Kugeln (1 bis 25). Es werden 5 Kugeln gezogen, ohne diese zurückzulegen. Wie viele Möglichkeiten gibt es, diese 5 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?)

3. In einer Urne befinden sich 10 durchnummerierte Kugeln (1 bis 10). Es werden 3 Kugeln gezogen, mit Zurücklegen. Wie viele Möglichkeiten gibt es, diese 3 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?

4. In einer Urne befinden sich 12 durchnummerierte Kugeln (1 bis 12). Es werden 4 Kugeln gezogen, mit Zurücklegen. Wie viele Möglichkeiten gibt es, diese 4 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?

5. Aus einem Skat-Kartenspiel (32 Karten) werden die Kreuzkarten herausgenommen. Es werden 3 Karten aus den verbleibenden 24 Karten gezogen, ohne Zurücklegen. Wie viele Möglichkeiten gibt es, diese 3 Karten zu ziehen, wenn die Reihenfolge keine Rolle spielt?

6. In einer Urne befinden sich 10 Kugeln mit den Zahlen 1 bis 10. Es werden 4 Kugeln gezogen, mit Zurücklegen. Wie viele Möglichkeiten gibt es, diese 4 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?

7. In einer Urne befinden sich 18 durchnummerierte Kugeln (1 bis 18). Es werden 6 Kugeln gezogen, ohne diese zurückzulegen. Wie viele Möglichkeiten gibt es, diese 6 Kugeln zu ziehen, wenn die Reihenfolge keine Rolle spielt?

8. Aus einem Skat-Kartenspiel (32 Karten) werden die Karo-Karten herausgenommen. Es werden 5 Karten aus den verbleibenden 24 Karten gezogen, mit Zurücklegen. Wie viele Möglichkeiten gibt es, diese 5 Karten zu ziehen, wenn die Reihenfolge keine Rolle spielt?

Diese App ist wurde erstellt von Dr. A. Rueff bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Links in diesem Ordner verweisen evtl. auf externe Inhalte.
Hinweise und Anregungen zur Aktualisierung dieser Seite oder zu Inhalten werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Vermischte Aufgaben: Permutationen, Variationen und Kombinationen

In einer Urne befinden sich 12 durchnummerierte Kugeln (1 bis 12). Es werden 5 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Kombinationen sind möglich, die bei dieser Ziehung gebildet werden können?
In einer Urne befinden sich 7 durchnummerierte Kugeln (1 bis 7). Es werden 4 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Reihenfolgen gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 10 durchnummerierte Kugeln (1 bis 10). Es werden 3 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen gibt es, die bei dieser Ziehung möglich sind?
Aus einem Skat-Kartenspiel (32 Karten) werden die Herz-Karten herausgenommen. Es werden 3 Karten aus den verbleibenden 24 Karten gezogen, ohne Zurücklegen. Wie viele verschiedene Kombinationen sind möglich?
In einer Urne befinden sich 15 durchnummerierte Kugeln (1 bis 15). Es werden 5 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 20 durchnummerierte Kugeln (1 bis 20). Es werden 4 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Kombinationen sind möglich?
In einer Urne befinden sich 8 durchnummerierte Kugeln (1 bis 8). Es werden 4 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen gibt es, die bei dieser Ziehung möglich sind?
Aus einem Kartenspiel (Skat, 32 Karten) werden die Pik-Karten herausgenommen. Es werden 3 Karten aus den verbleibenden 24 Karten gezogen, mit Zurücklegen. Wie viele verschiedene Reihenfolgen gibt es für diese Karten?
In einer Urne befinden sich 5 durchnummerierte Kugeln (1 bis 5). Es werden 3 Kugeln gezogen, ohne diese zurückzulegen. Wie viele verschiedene Reihenfolgen gibt es, die bei dieser Ziehung möglich sind?
In einer Urne befinden sich 6 durchnummerierte Kugeln (1 bis 6). Es werden 4 Kugeln gezogen, mit Zurücklegen. Wie viele verschiedene Kombinationen sind möglich?
In einer Urne befinden sich 10 Kugeln mit den Zahlen 1, 1, 1, 2, 2, 3, 4, 5, 6, 7. Wie viele verschiedene Reihenfolgen (Permutationen) gibt es?
In einer Urne befinden sich 7 Kugeln mit den Zahlen 2, 2, 3, 3, 3, 4, 5. Wie viele verschiedene Reihenfolgen (Permutationen) gibt es?

[Bild kann nicht geladen werden]

Mengenschreibweisen

[Bild kann nicht geladen werden]

→ Stochastik (2)

Erfahrungsbericht zu den Materialien:

Als geeignet hat sich u. a. der folgende Taschenrechner erwiesen:

Für die Oberstufe mit allen notwendigen Funktionen: Casio FX-991DE Plus (Dieser TR kann beispielsweise auch Integralrechnung, Vektorrechnung, Gleichungssysteme lösen, Statistik u.v.m.)

Using PhET Simulations in Teaching

Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0 (https://phet.colorado.edu).

Infotext ([05] Stochastik - Kombinatorik

Dieser Text basiert auf den Artikeln Kombinatorik und Kombination (Kombinatorik) aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.

Folie [03a]; [03b] - Erwartungswert

Beide Bilder: (c) Rueff - eigene Abbildungen

→ Rückmeldung geben