Technisches Zeichnen
Inhaltliche Informationen
Inhalt - Technisches Zeichnen
INHALTLICHE INFORMATIONEN
(Regeln, Daten, etc.)
- Allgemeine Informationen zur technischen Zeichnung
→ Das Papier
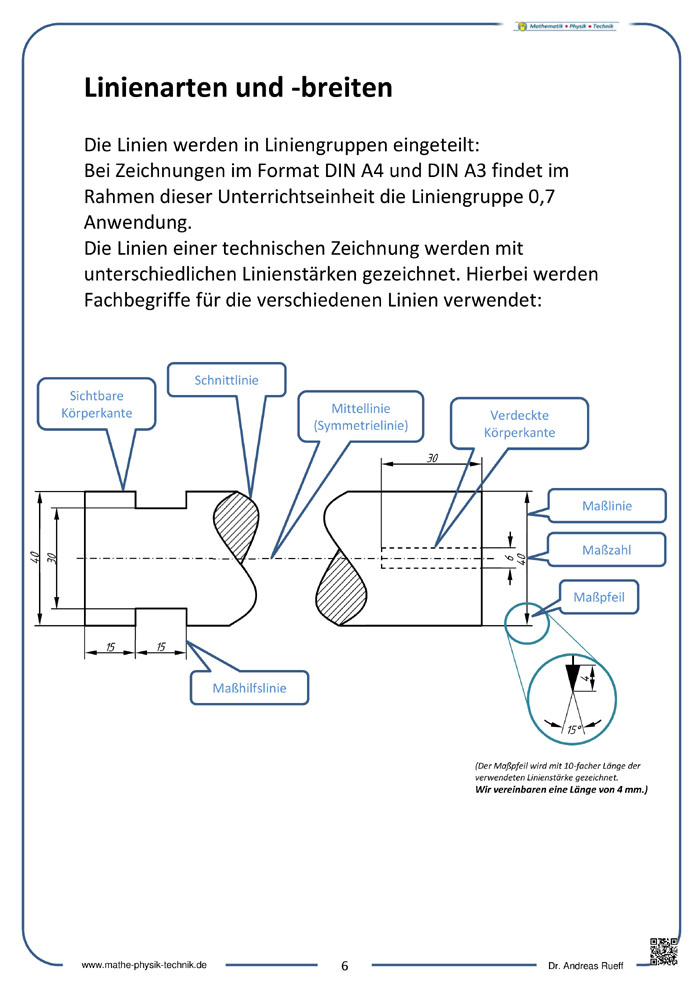
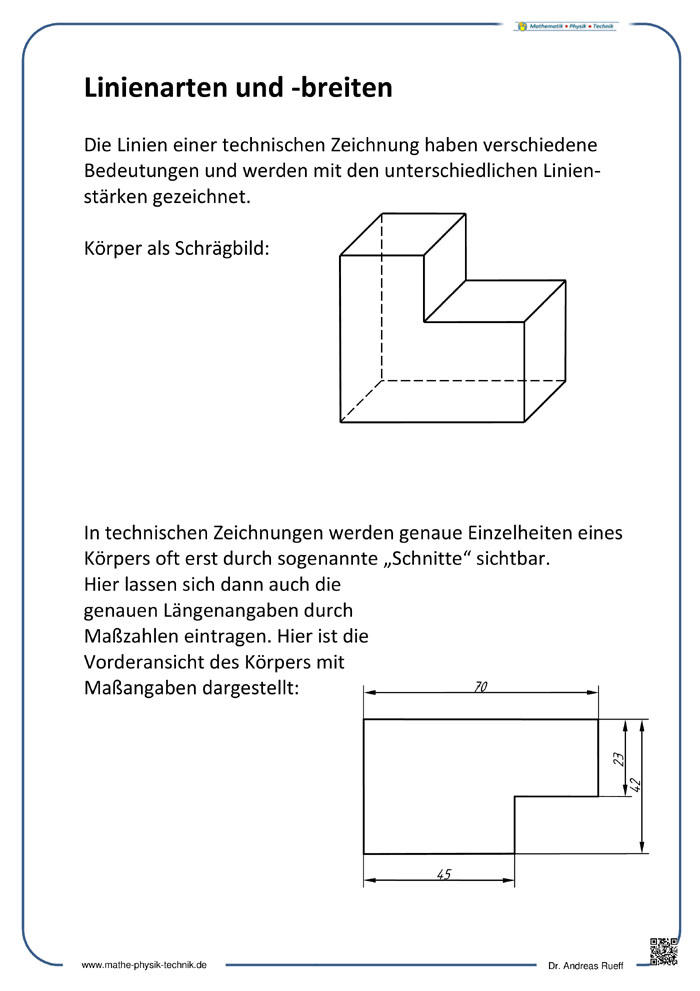
- Linienarten und Linienbreiten
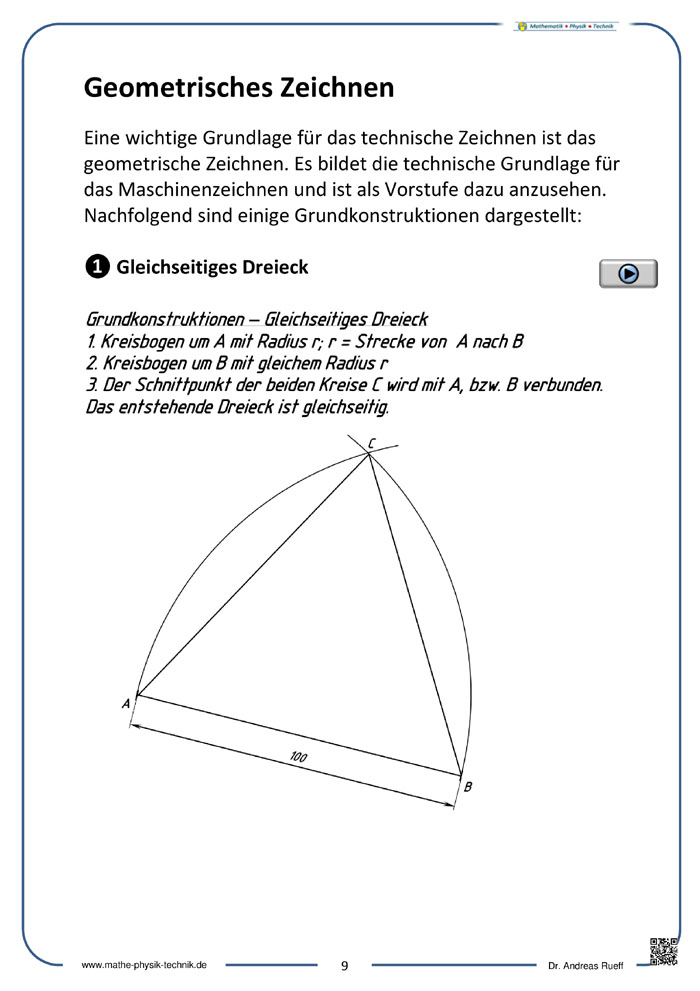
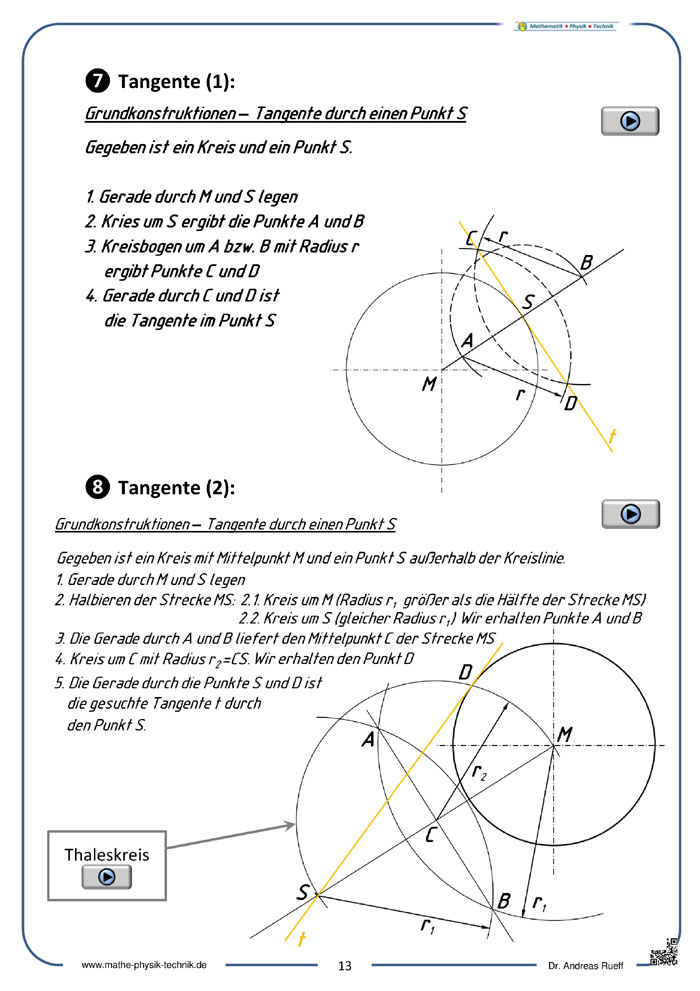
- Geometrisches Zeichnen
- Skizze und Zeichnung
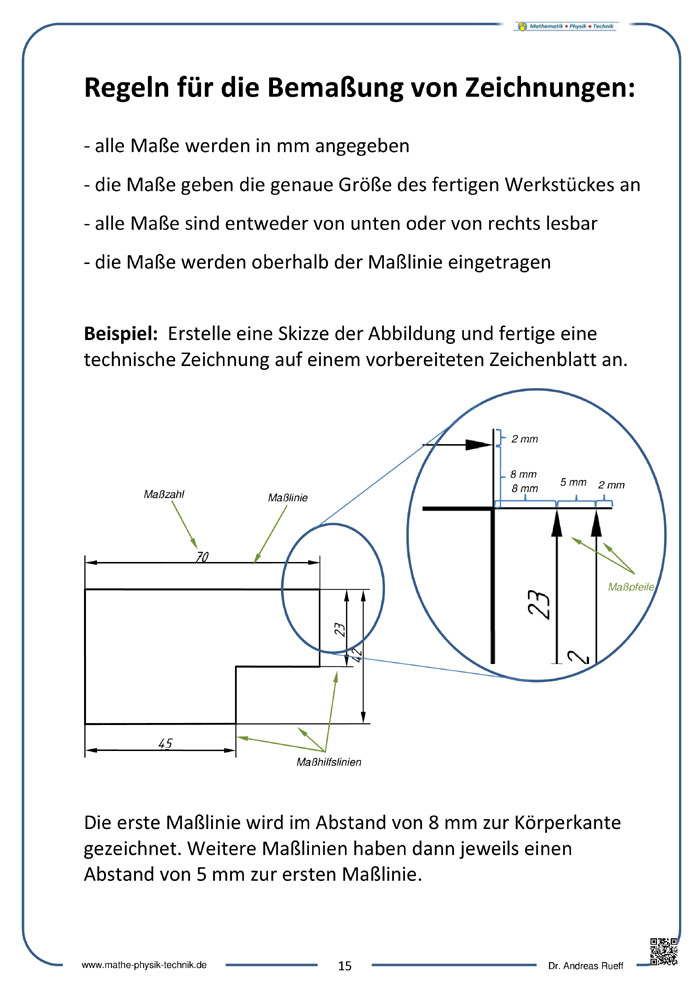
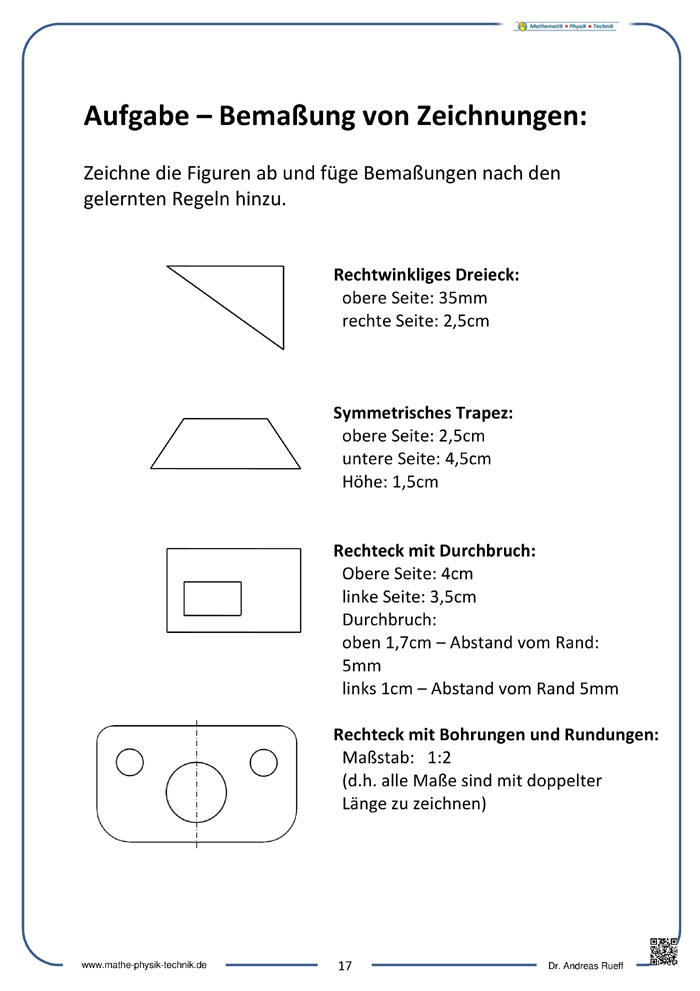
- Bemaßungsregeln
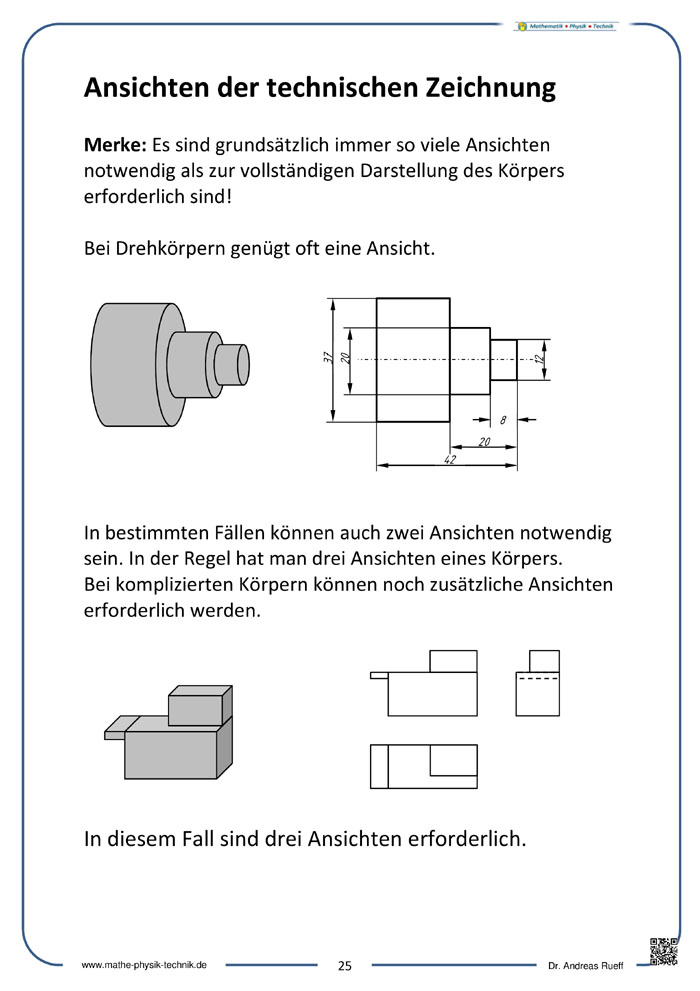
- Informationen zu Darstellungsarten
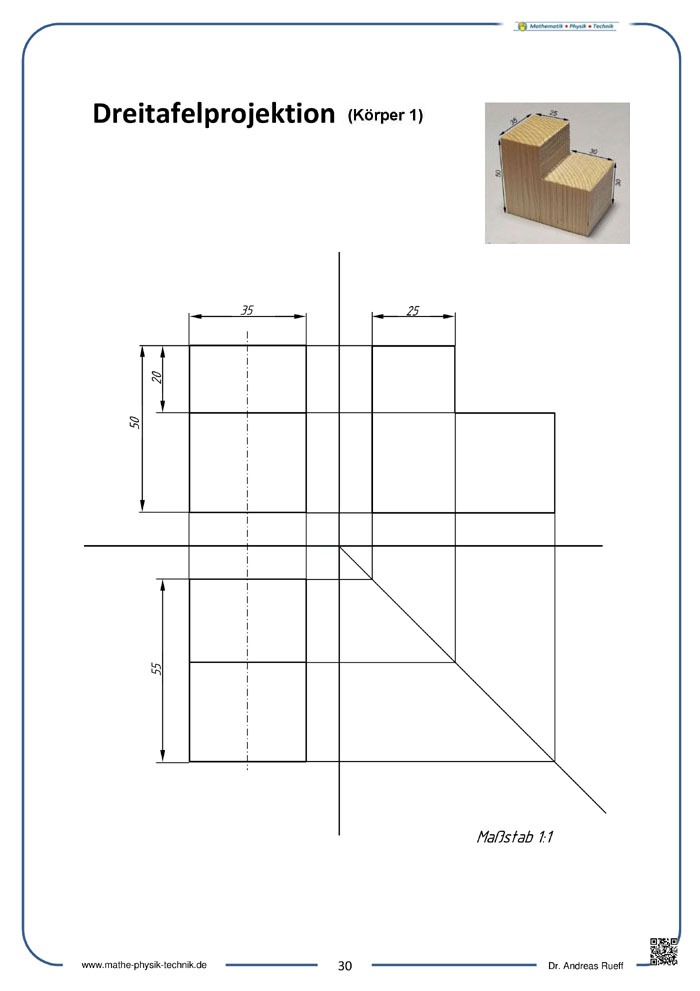
- Die Dreitafelprojektion
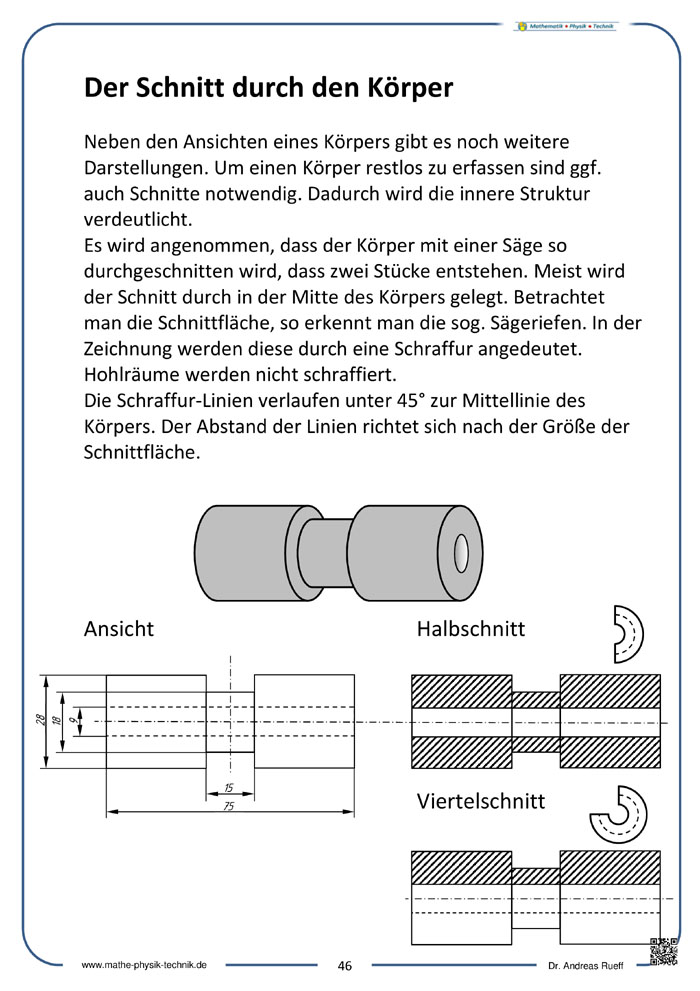
- Schnitte durch den Körper
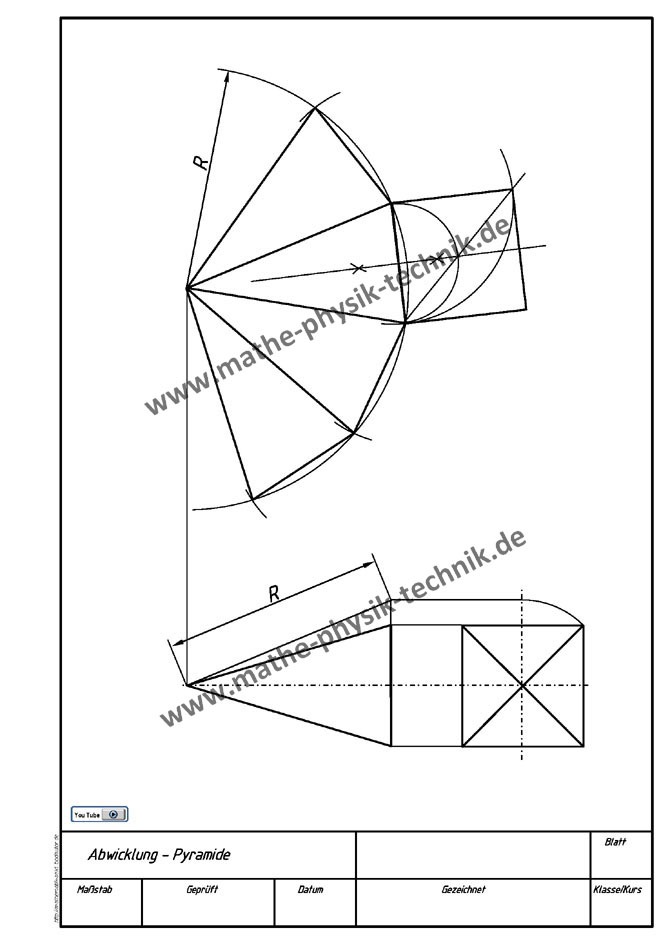
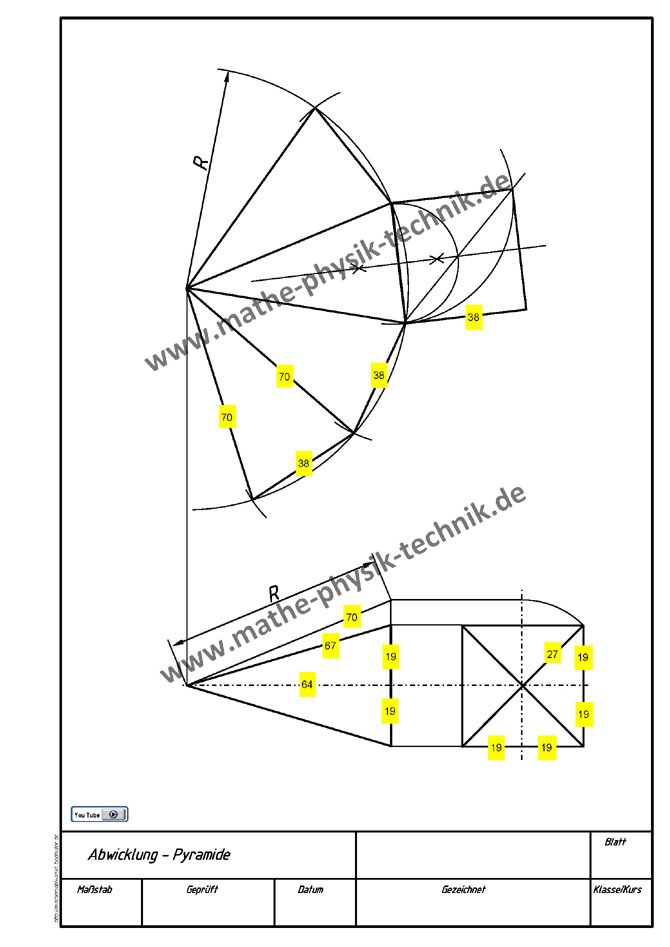
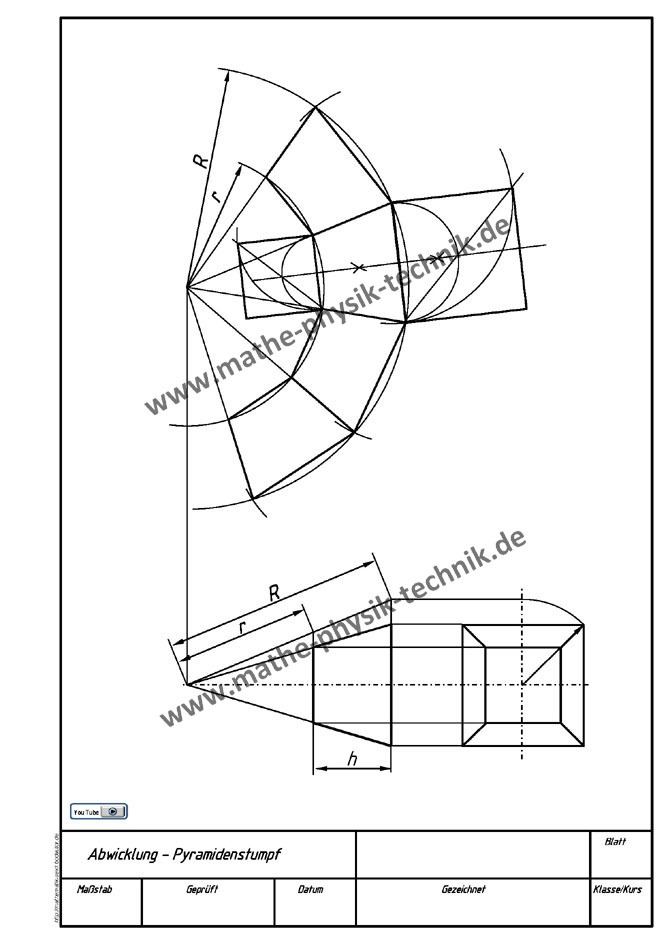
- Abwicklungen
a) Zeichenübungen
Übungen zur Arbeit mit Lineal, Zeichendreieck und Zirkel
b) Geometrisches Zeichnen (Zeichenvorlagen)
Strecke und Winkel halbieren, Streckenteilung, Tangenten konstruieren, Goldener Schnitt
c) Übungen zu den Darstellungsarten
Körper 1 - 6
Körper mit Nut
Kreise im perspektivischen Würfel
Schräg geschnittener Zylinder
Stangenkopf
Allgemeine Hinweise zu den Themenseiten
Die hier angebotenen Themenseiten fassen die grundlegenden Inhalte, Informationen und Hefteinträge zu den Unterrichtsinhalten von verschiedenen Themenbereichen der Fächer Mathematik, Physik und dem Wahlpflichtfach MINT/Technik zusammen. Diese sind online, kostenlos und ohne Registrierung verfügbar und sollen zur besseren Selbstorganisation der Schüler beitragen.
Die im Internet bereitgestellten Materialien bieten aber auch noch zusätzliche Möglichkeiten: Sie sollen den Schülern einen Leitfaden zur Vorbereitung auf Kursarbeiten, aber auch bei Fehlstunden zur Nacharbeit der versäumten Unterrichtsinhalte dienen und weiterhin den Eltern die Möglichkeit zur Unterstützung bei den unterrichtsbegleitenden Hilfestellungen geben. Die Zusammenfassungen zu den Unterrichtsinhalten auf den Themenseiten werden dabei jeweils ergänzt durch Lernvideos, Infotexten, Aufgaben, Bildergalerien und interaktiven Tools. Diese sollen dabei helfen selbstständig eigene Ergebnisse zu überprüfen oder zusätzliche Informationen zu den Inhalten erhalten. Bei den Lernvideos handelt es sich teilweise um die YouTube-Video des YT-Kanals Mathe-Physik-Technik. Weiterhin sind bei den einzelnen Folien zusätzliche Videovorschläge von anderen YouTube-Kanälen zugeordnet. Der jeweilige Link leitet dann ggf. direkt auf die YouTube-Video-Seite weiter.
Bei den klassischen physikalischen Themenbereichen sind die jeweiligen Folien für den digitalen Unterricht weitestgehend angepasst und optimiert worden. Insbesondere durch die Corona-Krise rückt der digitale und eigenverantwortliche Unterricht immer mehr in den Fokus. Zu den einzelnen Folien sind deshalb jeweils passende Videos zu den Inhalten zugeordnet und zu vielen Folien auch passende Aufgaben eingearbeitet worden. Dadurch sind die Themenbereiche in Teilabschnitten strukturiert und für die Arbeit mit Wochenplänen optimiert worden. Sie ermöglichen den Schülern so die selbstständige Arbeit daheim und geben jedem Schüler die Möglichkeit die Lernziele auch unter den gegebenen Umständen bestmöglich zu erreichen. Dabei können Schüler dann sogar die positiven Seiten des digitalen Unterrichts (Eigenes Lerntempo festlegen, optimale Anpassung von Lernzeit und Zeitpunkt an den eigenen Biorhythmus zum effizienten Lernen, etc.) für sich besonders gut nutzen.
Siehe hierzu auch: → Konzept - mathe-physik-technik.de
Skript → Publikationen

Die Technische Zeichnung (Normen)
Die Technische Zeichnung ist die „Sprache“ der Ingenieure.
Eine Technische Zeichnung ist ein grafisches Dokument, das vorwiegend im Maschinenbau und im Anlagenbau verwendet wird und zum Teil auch in schriftlicher Form die für die Herstellung eines Einzelteils oder die Montage zu einer Baugruppe oder der kompletten Maschine erforderlichen Informationen enthält. Sie dient auch als Teil der technischen Produktdokumentation.

DIN 199 definiert dazu folgendes: „Eine Technische Zeichnung ist eine Zeichnung in der für technische Zwecke erforderlichen Art und Vollständigkeit, z. B. durch Einhaltung von Darstellungsregeln und Maßeintragungen.“
Diese Definition trägt dem komplexen Prozess Rechnung, der zur Erstellung vollständiger, normgerechter Technischer Zeichnungen erforderlich ist und Technisches Zeichnen genannt wird. Für technische Zeichnungen wird immer auch ein passendes Papier mit einem Zeichnungsrand und ein Schriftfeld für die Bezeichnung des Objekts und weitere Zusatzinformationen (Datum, Name, Maßstab, …). Das verwendete Papier ist dafür oft stabiler als das normale Kopierpapier, es hat anstelle der 80g/m² dann beispielsweise 150g/m² oder 200g/m² (Zeichenkarton). Weiterhin wird auch oft transparentes Zeichenpapier verwendet (ähnelt dem oft im Alltag verwendeten „Butterbrotpapier“).
Was sind „Normen“?
Der Begriff Normung bezeichnet die Formulierung, Herausgabe und Anwendung von Regeln, Leitlinien oder Merkmalen durch eine anerkannte Organisation und deren Normengremien (Gremien sind Gruppen von mehreren Experten auf einem bestimmten Wissensgebiet). Sie sollen auf den gesicherten Ergebnissen von Wissenschaft, Technik und Erfahrung basieren und auf die Förderung optimaler Vorteile für die Gesellschaft abzielen. Die Festlegungen werden mit Konsens erstellt und von einer anerkannten Institution angenommen. Das Deutsche Institut für Normung e. V. (DIN) ist die bedeutendste nationale Normungsorganisation in der Bundesrepublik Deutschland. Sie wurde am 22. Dezember 1917 unter dem Namen „Normenausschuß der deutschen Industrie“ gegründet. Das heutge Arbeitsgebiet beschränkt sich aber nicht nur auf die Industrie. Der heutige Name „DIN Deutsches Institut für Normung e. V.“ wurde 1975 im Zusammenhang mit dem zwischen der Organisation und der Bundesrepublik Deutschland abgeschlossenen Normenvertrag gewählt. Eine unter der Leitung von Arbeitsausschüssen dieser Normungsorganisation erarbeitete Norm wird als DIN-Norm bezeichnet. Die oben genannte „DIN 199“ ist ein Beispiel dafür. Im Bereich der Technischen Zeichnungen geben die DIN-Normen Vorgaben für die Bedeutung bestimmter Linienarten (z.B.: Volllinie, Strichlinie, Strichpunktlinie, …) und die Strichstärken (Breite einer Linie). Auch die Größe von Papier ist durch DIN-Normen eindeutig festgelegt. Im Alltag ist uns beispielsweise das Papierformat DIN-A4 allen bekannt.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Die Technische Zeichnung (Darstellungarten)
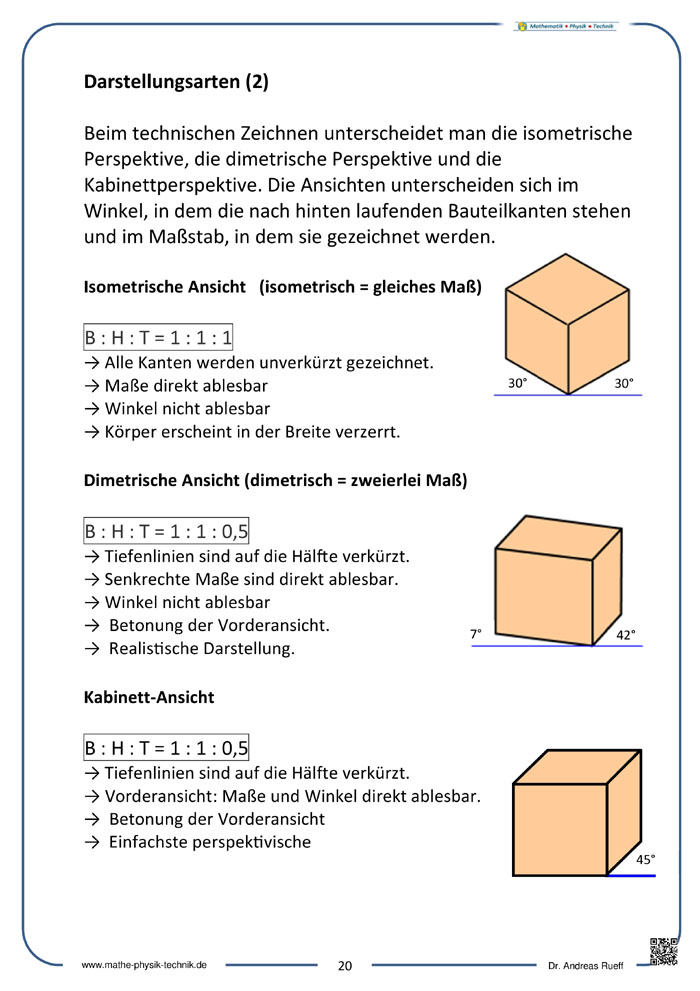
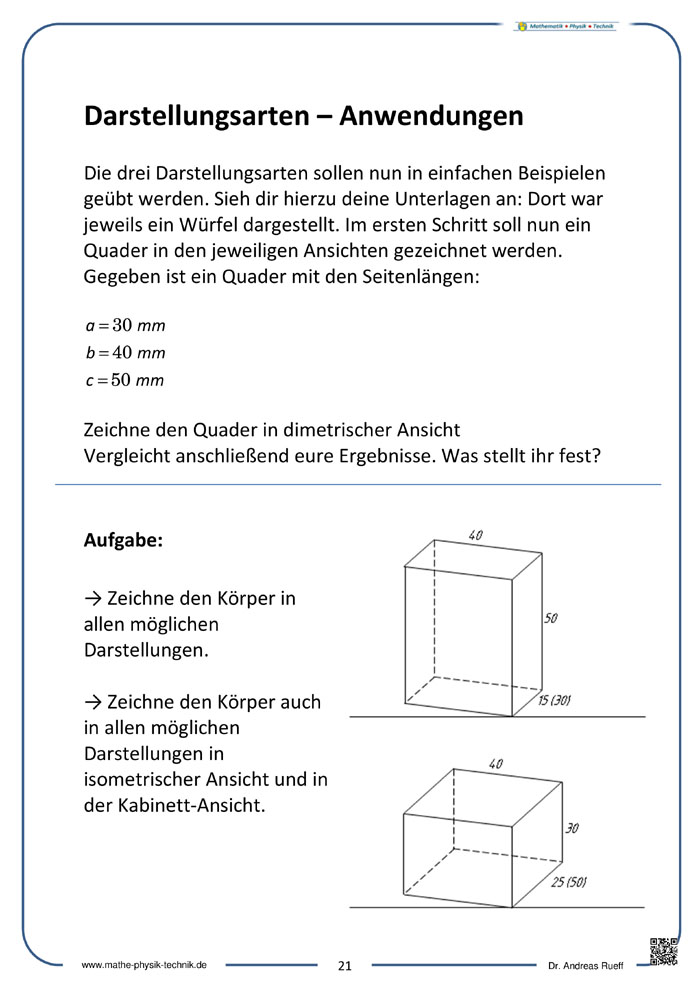
Darstellungsarten
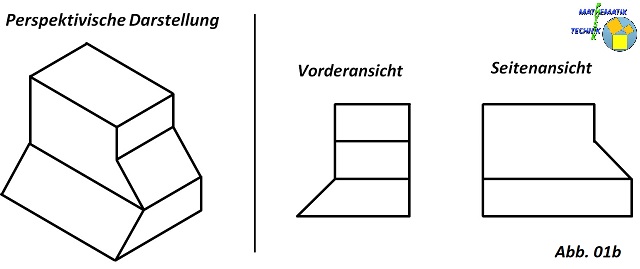
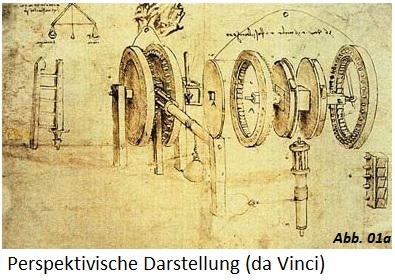 In den frühesten Zeichnungen wurde die anschauliche perspektivische (dreidimensionale) Darstellung benutzt (siehe
Abb. 01a). Weil sie relativ hohe Anforderungen an die Begabung der Zeichner stellt und zudem die Objekte teilweise verzerrt darstellen, ging man bei Beginn der
Industrialisierung (18. Jahrhundert) auf zweidimensionale Abbildungen der Objekte über. Viele Kanten der meisten technischen Gegenstände sind untereinander rechtwinklig
angeordnet. Man kann deshalb von den Objekten relativ leicht verschiedene Ansichten (Vorder-/Rückansicht, Seitenansicht, Draufsicht, ...) anfertigen. Die Flächen werden dabei
unverzerrt abgebildet. Nachteilig ist, dass sich der Betrachter die Geometrie des Körpers aus mehreren Ansichten vorstellen muss (setzt räumliches Vorstellungsvermögen
voraus).
In den frühesten Zeichnungen wurde die anschauliche perspektivische (dreidimensionale) Darstellung benutzt (siehe
Abb. 01a). Weil sie relativ hohe Anforderungen an die Begabung der Zeichner stellt und zudem die Objekte teilweise verzerrt darstellen, ging man bei Beginn der
Industrialisierung (18. Jahrhundert) auf zweidimensionale Abbildungen der Objekte über. Viele Kanten der meisten technischen Gegenstände sind untereinander rechtwinklig
angeordnet. Man kann deshalb von den Objekten relativ leicht verschiedene Ansichten (Vorder-/Rückansicht, Seitenansicht, Draufsicht, ...) anfertigen. Die Flächen werden dabei
unverzerrt abgebildet. Nachteilig ist, dass sich der Betrachter die Geometrie des Körpers aus mehreren Ansichten vorstellen muss (setzt räumliches Vorstellungsvermögen
voraus).
Beim Technischen Zeichnen mit einem Computer (CAD; computer-aided design zu Deutsch rechnerunterstütztes Konstruieren) lässt sich inzwischen ohne besonderen Aufwand jede
beliebige perspektivische Darstellung erzeugen.
Siehe hierzu auch: Bildergalerie 1 - Technisches Zeichnen früher und heute.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
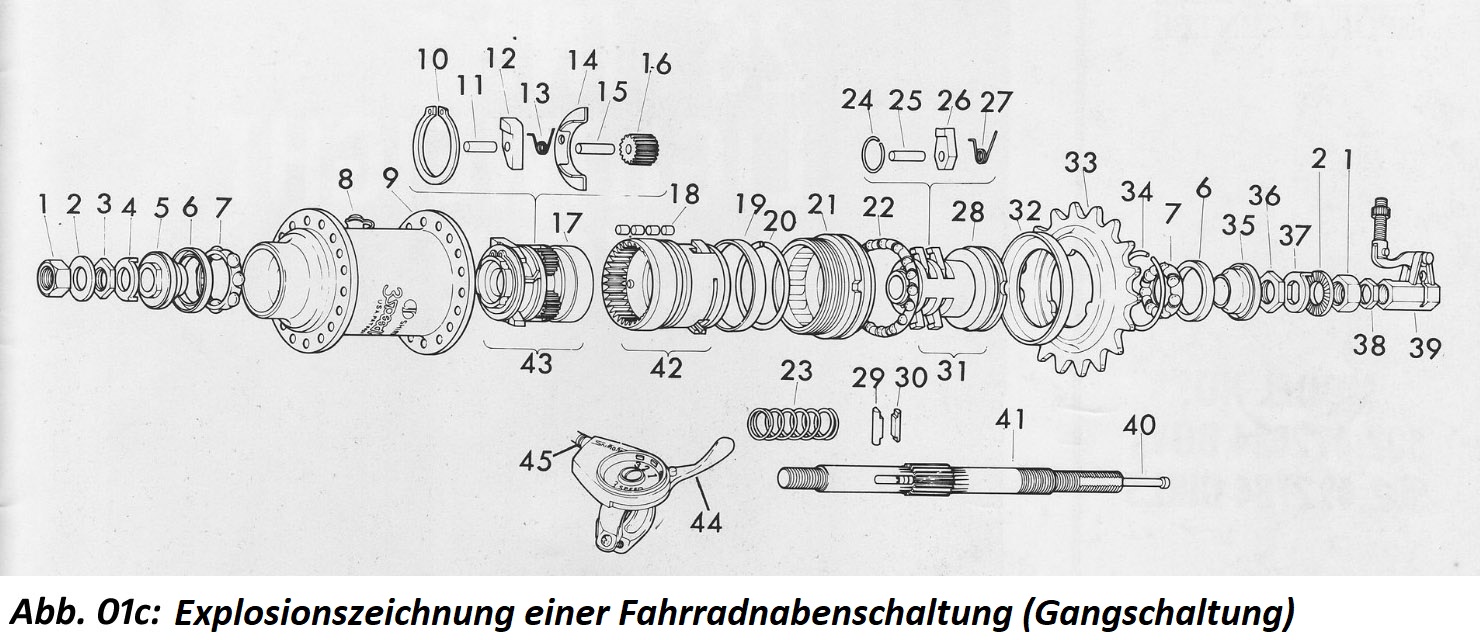
Die Explosionszeichnung
Eine Explosionszeichnung (auch Explosionsgrafik, Explosivdarstellung) ist eine Art der Darstellung bei Zeichnungen und Grafiken, die einen komplexen Gegenstand in seine Einzelteile zerlegt zeigt (u. a. auch perspektivisch dargestellt). In Fachkreisen wird hier auch die Formulierung Sprengzeichnung verwendet. Die dargestellten Einzelteile oder Bauteile sind räumlich voneinander getrennt, d. h. so, als flögen sie nach einer Explosion auseinander.
Bei dieser Darstellungsweise wird das Wechselverhältnis des Ganzen zu seinen Teilen sowie deren Lage verdeutlicht. Explosivdarstellungen erlauben es, die Funktion und den Zusammenbau von Baugruppen darzustellen sowie einzelne Bauteile anhand mit angegebener Teilenummern zu bestimmen, z. B. aus der Gesamtabbildung zum gesuchten Ersatzteil und seiner Lagernummer.
Diese Art der Darstellung findet in verschiedenen Bereichen Verwendung: Als Informationsgrafik kommt diese Darstellungsart in Gebrauchsanweisungen und Ersatzteil-Katalogen (auch virtuellen, interaktiven Katalogen) zum Einsatz. Bei Montageanleitungen wird mit Explosionsgrafiken die Montage- und Demontagereihenfolge einzelner Teile erklärt. In technischen Zeichnungen im Maschinenbau werden komplexe Maschinen auf diese Weise übersichtlich dargestellt.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.

Hinweis zu den Zeichengeräten
Es kann - je nach verfügbarer Wochenstundenzahl - die folgende Vereinbarung getroffen werden: Die Anschaffung aller hier (Folie 01b) genannten Materialien ist im Rahmen einer halbjährigen
Unterrichtseinheit nicht notwendig! Es wird dafür aber mindestens ein Feinminenstift (0,5mm), ein Geodreieck und ein weiteres Zeichendreieck
(oder Lineal) und altenativ zu den echten Tuschestiften (relativ teuer!) ein Grafik-Fineliner-Stifteset mit drei Strichstärken (0,3mm, 0,5mm, 0,7mm) vorausgesetzt.
Ausdrückliche Bitte und Empfehlung: Bitte unterstützt die heimische Wirtschaft und kauft die Materialien in einem ortsansässigen Geschäft oder dem jeweiligen Online-Shop! Nachfolgend sind Produkthinweise gezeigt. Diese sollen in erster Linie dazu dienen, dass die richtigen Materialien gekauft werden. Vergleichbare Produkte gibt es im Schreibwarenhandel auch bei euch um die Ecke.
Danke!
Hinweis zur Vorgehensweise beim Erstellen der Zeichnungen
Verwende für deine Zeichnungen zum Einstieg (Zeichenübungen 1a,b,c) nur den Feinminenstift (Bleistift). Für die weiteren Zeichnungen und Zeichenübungen soll dann immer zunächst mit dem Feinminenstift (Bleistift) vorgezeichnet werden. Zeichne dann zur Fertigstellung die Zeichnungen mit den Grafik-Fineliner-Stiften (oder Tuschestiften) deine Zeichnung nach und entferne anschließend ggf. die Reste der Bleistiftlinien. Achte beim Vorzeichnen mit dem Bleistift darauf, dass du nicht zu viel Druck auf den Stift ausübst. Deine Bleistiftlinien sollten mit einem Radiergummi wieder vollständig entfernt werden können. Übe das zunächst auf einem Schmierblatt und beginne dann mit deinen Zeichenübungen.
Produkthinweise
Faber-Castell 1345 99 - Druckbleistift GRIP, Minenstärke: 0,5 mm, Schaftfarbe: schwarz metallic
|
rOtring 3-teiliges Tikky-Grafik-Fineliner-Stifteset
|
Radierer TB 20 Tusche Blei R551320A |
→ Hinweise zur Ausbildung als Technische/r Zeichner/in (www.ausbildung.de)
→ YT-Video: Berufsbild: Technisches Zeichnen [1:15]
→ YT-Video: Ausbildung als Technische/r Zeichner/in [8:07]
Diese externen Links führen zur Seite: www.ausbildung.de bzw. auf das entsprechende YouTube-Video.

Bildergalerie 1 - Technisches Zeichnen früher und heute

Technisches Zeichnen - Die Parallelverschiebung:
Zeichentechnik für parallel verlaufende Strecken in einer Zeichnung [5:55]
Dargestellt wird die zeichnerische Technik der Parallelverschiebung bei Zeichnungen mit parallel verlaufenden Strecken. Er werden zwei Beispiele gezeigt: Eine zweidimensionale und eine dreidimensionale Zeichnung.

Die Normschrift
Eigenschaften der Schrift nach DIN EN ISO 3098
Die Schrift nach DIN EN ISO 3098 hat keine im spitzen Winkel zusammenlaufenden Linien. Sie gibt es sowohl in der geraden, als auch in einer um 15° schräg (kursiv) gestellten Form. Einfach umsetzen lässt sich die Normschrift mit Hilfe einer Schriftschablone.
Es sind drei genormte Größen von Groß- und Kleinbuchstaben und Strichstärke mit folgenden Werten gebräuchlich.
Strichstärke 0,25 mm:
Schriftgröße h=2,5 mm
Höhe der Kleinbuchstaben 1,75 mm
Strichstärke 0,5 mm:
Schriftgröße h=5 mm
Höhe der Kleinbuchstaben 3,5 mm
Strichstärke 0,7 mm:
Schriftgröße h=7 mm
Höhe der Kleinbuchstaben 4,9 mm
Die Zeilen, in denen in Normschrift geschrieben wird, bestehen aus einer Ober- und Unterzeile für die Großbuchstaben sowie einer Mittelzeile für die Kleinbuchstaben.
Heutige Bedeutung händischen Beschriftens
In der heutigen Zeit, in der viele technische Zeichnungen mit dem Computer erstellt werden, ist es nicht mehr zwingend notwendig das händische Beschriften in
Normschrift zu beherrschen. Jedoch sollte man dennoch mit den Grundlagen vertraut sein, um beispielsweise bei Handskizzen ein sauberes Schriftbild zu
erhalten. Dabei sollte dann die Normschrift weitestgehend nachempfunden werden – falls keine Normschriftschablone zur Verfügung steht aber per Hand beschriftet wird.
Erlernt wird die Normschrift mit Hilfe von Schriftschablonen, die Durchbrüche für Buchstaben, Ziffern usw. enthalten, die dann nacheinander geschrieben werden, um die
Schriftbewegung zu erlernen. Danach werden die Buchstaben freihand abgeschrieben.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
→ Zeichentechnik: Video und Vorlage zur Zeichenübung 1a,b (Folie 22/23)
→ Zeichentechnik: Video und Vorlage zur Zeichenübung 1c,d,e (Folie 24-26)

→ Zeichentechnik: Video und Vorlage zur Zeichenübung 2a,b (Folie 27/28)

→ Zeichentechnik: Video und Vorlage zur Zeichenübung 2c (Folie 29)
Geometrisches Zeichnen
(Siehe hierzu auch: Zeichentechnik - Vorlagen 32-39)
Der Goldene Schnitt

Weitere Videos zu Grundkonstruktionen / Geometrisches Zeichnen sind auf der Seite Lern-Archiv zusammengefasst.
Vorschläge für Übungszwecke:
→ Zeichentechnik: Video und Vorlage zur Zeichenübung 3a,b (Folie 30/31)
Perspektifische Darstellungen
Perspektive (von lateinisch perspicere ‚hindurchsehen, hindurchblicken‘) bezeichnet die räumlichen, insbesondere linearen Verhältnisse von Objekten im Raum: das
Abstandsverhältnis von Objekten im Raum in Bezug auf den Standort des Betrachters.  Damit ist die Perspektive stets an den Ort des Betrachters gebunden und kann nur durch Veränderung der Orte der
Objekte und des Betrachters im Raum verändert werden. Die perspektivische Darstellung fasst die Möglichkeiten zusammen, dreidimensionale Objekte auf einer zweidimensionalen Fläche so
abzubilden, dass dennoch ein räumlicher Eindruck entsteht. Sehr oft verwendet wird im künstlerischen Bereich die Zentralperspektive (vgl. Abb.06.1), weiterhin ist auch
beispielsweise die Froschperspektive eine oft verwendete Darstellungsart (Abb. 06.2).
Damit ist die Perspektive stets an den Ort des Betrachters gebunden und kann nur durch Veränderung der Orte der
Objekte und des Betrachters im Raum verändert werden. Die perspektivische Darstellung fasst die Möglichkeiten zusammen, dreidimensionale Objekte auf einer zweidimensionalen Fläche so
abzubilden, dass dennoch ein räumlicher Eindruck entsteht. Sehr oft verwendet wird im künstlerischen Bereich die Zentralperspektive (vgl. Abb.06.1), weiterhin ist auch
beispielsweise die Froschperspektive eine oft verwendete Darstellungsart (Abb. 06.2).

Darstellende Geometrie
Die Darstellende Geometrie ist der Teilbereich der Geometrie, der sich mit den geometrischen Verfahren zur Darstellung dreidimensionaler Objekte auf eine
zweidimensionale Darstellungsebene befasst. Das bedeutet, dass dreidimensionale Gegenstände auf einem zweidimensionalen Platt Papier möglichst realistisch
dargestellt werden sollen. Die Anwendungsbereiche der Methoden sind breit gefächert und erstrecken sich neben den heute bekanntesten Anwendungen in der Technik- und
Architekturdarstellung auch auf Kunst, Malerei, Kartenwesen und Computergraphik. Die Darstellende Geometrie beschränkt sich nicht nur auf das Darstellen von räumlichen Objekten,
sondern bietet auch Möglichkeiten raumgeometrische Probleme zeichnerisch zu lösen: z. B. die Bestimmung des Schnittpunktes einer Gerade mit einer Ebene oder die Schnittkurve zweier Flächen
oder den Schatten eines Objektes.
Im Gegensatz zu früher ist die Darstellende Geometrie nicht mehr das einzige Mittel, um räumliche Objekte anschaulich darzustellen oder raumgeometrische Probleme zu lösen.
Hierfür verwendet man heute Computer. Die Bedeutung der Darstellenden Geometrie liegt heute vielmehr im Training der Benutzer geometrischer Software, damit
sie verstehen, was eine Software kann und an Eingaben verlangt. Für erste Skizzen einer (räumlichen) Idee oder Interpretationen und Ergänzungen von Computerzeichnungen ist das
Zeichnen mit Zirkel und Lineal eine sehr gute Übung.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Perspektive - erklärt in 3 Minuten [3:05]
2) → Perspektive - Fluchtpunkt [4:48]
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!
Abbildungsverfahren
In der Darstellenden Geometrie bedient man sich im Wesentlichen zweier Abbildungsverfahren. Dabei werden Punkte und Kurven eines Objektes mit Hilfe von Strahlen (Geraden) auf eine Bildtafel (Ebene) projiziert:
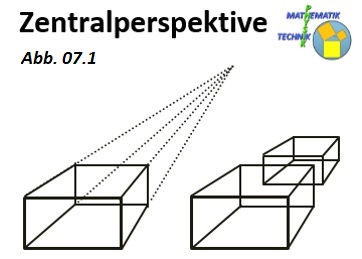 Zentralperspektive
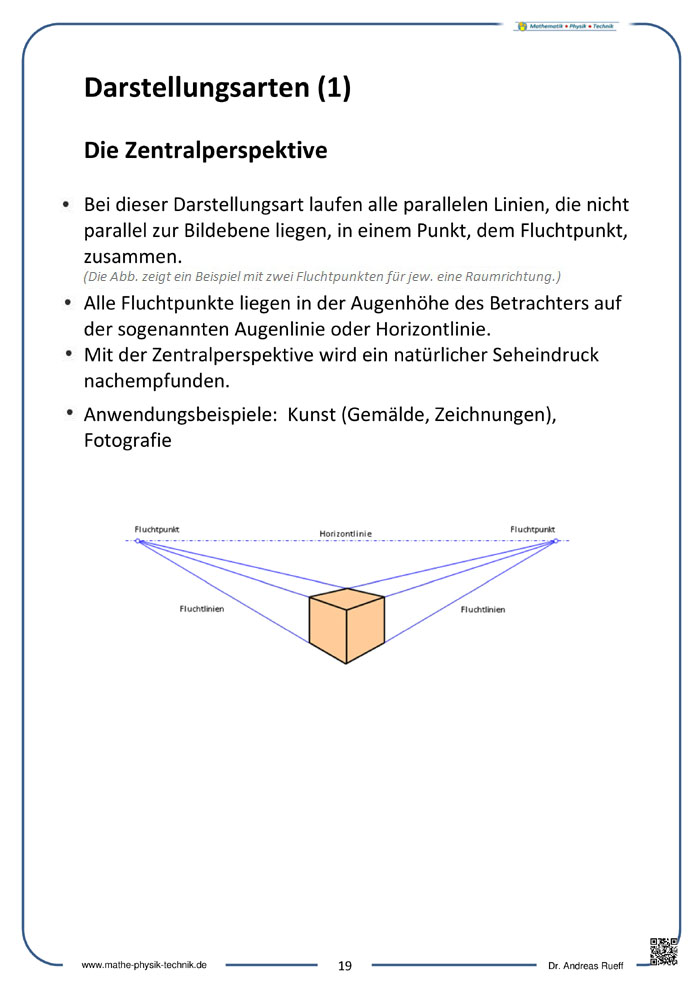
Zentralperspektive
Bei Zentralperspektive (auch Zentralprojektion) verlaufen parallel liegende Kanten in der zweidimensionalen Darstellung so, dass die Verlängerung der Kanten i. A. auf
einen Punkt (den Fluchtpunkt) zulaufen. Parallele Kanten sind in der Darstellung also nicht mehr parallel. Das führt dann zu einer realistischeren Darstellung, die
Messung von Abständen in der Zeichnung ist aber dadurch nicht mehr möglich.
Dass eine Zentralperspektive den besten optischen Eindruck verschafft, zeigen die Bilder der Eisenbahnschienen. Die Schienen haben immer den gleichen Abstand. Sie laufen aber
in der Darstellung auf einen Punkt zu.

Parallelperspektive
Bei der Parallelperspektive verlaufen parallele Kanten immer auch in der zweidimensionalen Darstellung parallel. Parallelperspektiven werden gerne von Ingenieuren verwendet
wegen ihrer Teilverhältnistreue (Teilverhältnisse auf Geraden bleiben unverändert. In der Abbildung sieht man das daran, dass die Quader bei gleicher Kantenlänge auch die
gleichen Längen in der Abbildung aufzeigen. Es spielt also keine Rolle, ob in der Abbildung die Kantenlänge des ersten, zweiten oder dritten Quaders gemessen/gezeichnet wird.). Die
Parallelperspektive lässt sich relativ einfach von Hand herstellen. Auf der Parallelperspektive beruhen die technischen Zeichnungen der Ingenieure und Architekten. 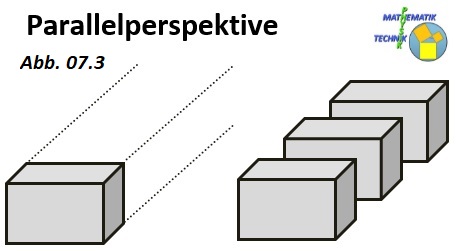 Spezielle Varianten sind die
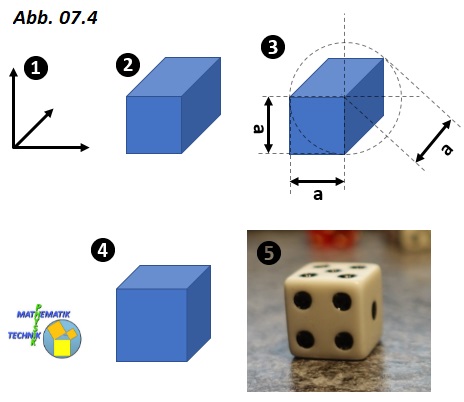
isometrische, die dimetrische und die Kabinett-Ansicht. Dabei wird eine möglichst realistische Darstellung der Körper angestrebt. Dies ist aber ohne die
Verzerrung eine Bildachse nicht möglich. Das lässt sich am Beispiel eines Würfels zeigen:
Spezielle Varianten sind die
isometrische, die dimetrische und die Kabinett-Ansicht. Dabei wird eine möglichst realistische Darstellung der Körper angestrebt. Dies ist aber ohne die
Verzerrung eine Bildachse nicht möglich. Das lässt sich am Beispiel eines Würfels zeigen:
Die drei Raumrichtungen in der zweidimensionalen Darstellung sind in der Abbildung zunächst du drei Koordinatenachsen dargestellt. Ein Würfel in der zweidimensionalen
Darstellung sieht unter der Voraussetzung, dass alle drei Kanten mit gleicher Länge gezeichnet werden sehr unrealistisch aus (Tailabb. 2 und 3). In der Teilabb. 4
hingegen entspricht die Darstellung sehr gut der Fotografie in Teilabbildung 5. Dabei werden aber Verzerrungen vorgenommen. Die nach hinten weisende Raumrichtung wird hier
verkürzt dargestellt. Dadurch entsteht der richtige räumlich Eindruck eines Würfels.
-----------------------------------
Hinweis: Die Quellenangaben zu diesem Text sind am Ende dieser Internetseite zu finden.
Videos:
1) → Die Zentralperspektive [5:05]
2) → Fluchtpunktperspektive/ Zentralperspektive Erklärvideo [8:45]
Anmerkung: Die Links in diesem Ordner verweisen auf externe YouTube-Videos anderer YouTube-Kanäle. Gelegentlich werden Videos dort auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite werden gerne per → Mail oder über das → Kontaktformular entgegengenommen. - Vielen Dank schon vorab für den Hinweis!

Schrägbilder - Kabinett-Ansicht: [6:47]
Gezeigt wird die Konstruktion von Schrägbildern - Mathematik, Mittelstufe. Dabei werden die grundlegenden Regeln eingeführt und beschreiben. Anschließend werden zwei Beispiele mit allen
notwendigen Einzelheiten vorgeführt: 1) Ein Quader und 2) ein Dreiecksprisma.
Diese Darstellungsart wird auch als Kabinett-Ansicht bezeichnet.

Wiederholung: Winkel messen [8:55]
Zunächst werden einige Grundbegriffe des Geodreiecks eingeführt. Anschließend wird an einem Beispiel die Winkelmessung demonstriert. Dabei wird auf die beiden Winkelskalen am Geodreieck eingegangen und es werden zwei Varianten zur Winkelmessung dargestellt. Hierbei finden beide Skalen Anwendung zur Messung des Winkels.

Wiederholung: Winkel zeichnen [3:45]
Anschaulich beschrieben wird die Vorgehensweise beim Zeichnen eines Winkels. Hierbei wird ein spitzer und ein stumpfer Winkel als Beispiel gezeichnet.
(Zur Darstellung der Isometrischen und dimetrischen Ansicht)


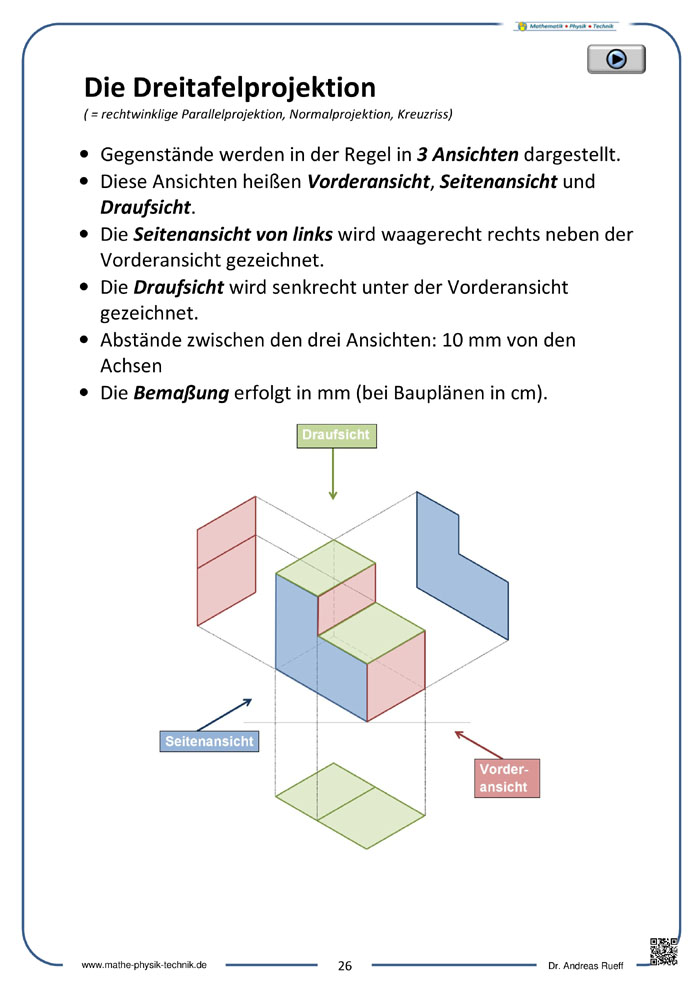
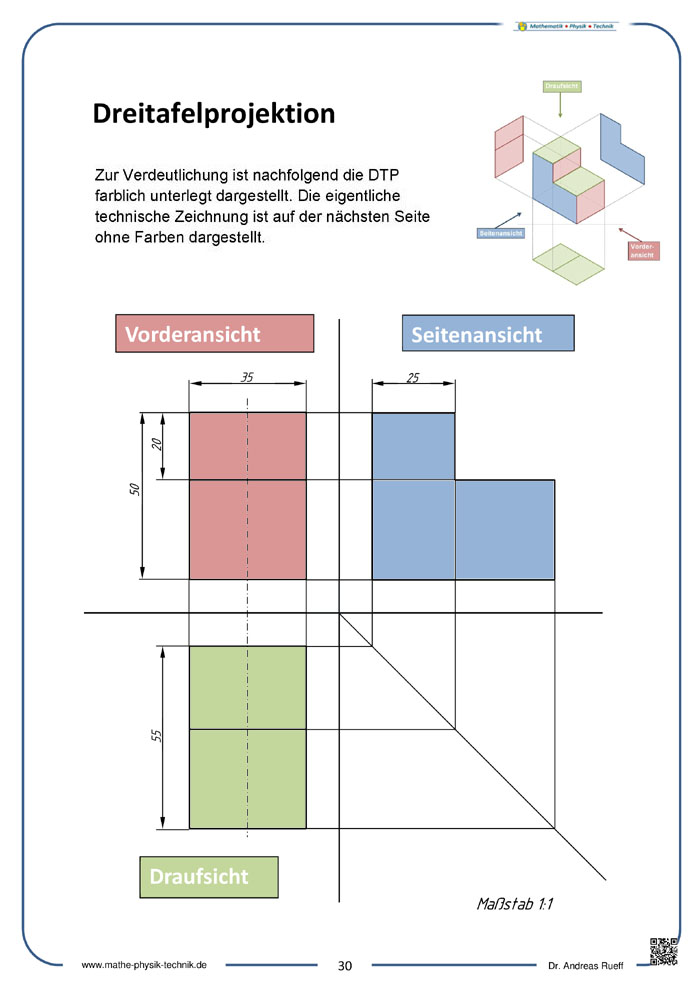
Dreitafelprojektion (DTP)
Diese App basiert auf einer App von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App basiert auf einer App von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App basiert auf einer App von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App basiert auf deiner App von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
Diese App basiert auf einer App von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!
→ Zeichentechnik: Übungen zu den Darstellungsarten und zur DTP (Folie 40-48)

Ein animiertes Video mit Informationen zur Abwicklung eines Körpers (Beispiel: Quader und Würfel) findest du hier:
Diese Online-Übung ist eine extern eingebundene App von Sabine Jung.
Diese App wurde erstellt von Sabine Jung bei LearningApps.org
Anmerkung: Die Online-Übung in diesem Ordner ist eine externe Übung. Angaben zum Ersteller sind teilweise (manchmal) auch in der Übung angegeben. Links in diesem Ordner
verweisen evtl. auf externe Inhalte.
Gelegentlich werden Übungen vom Ersteller auch wieder entfernt. Entsprechende Hinweise zur Aktualisierung dieser Seite oder auch Hinweise zu Inhalten werden gerne per
→ Mail
oder über das → Kontaktformular entgegengenommen. - Vielen Dank
schon vorab für den Hinweis!

Videos zu technischen Grundkonstruktionen, Zeichenübungen, etc. sind auf der Seite Lern-Archiv zusammengefasst oder als Playlist auf dem YouTube-Kanal zu sehen.


Alle von mir erstellten Materialien stehen für Bildungszwecke frei zur Verfügung, dürfen allerdings nicht von jemand anderem kommerziell vertrieben werden.
Hinweis: Es werden keine Bücher oder sonstige, hier benannte Materialien im Unterricht verwendet oder benötigt.
Quellenangaben zu den Inhalten auf dieser Seite
Infotext ([01.1] Die technische Zeichnung - Normen)
 Dieser Text basiert auf den Artikeln Technische Zeichnung, Papierformat, Deutsches
Institut für Normung und Normung aus der freien Enzyklopädie Wikipedia und steht unter der
Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Technische Zeichnung, Papierformat, Deutsches
Institut für Normung und Normung aus der freien Enzyklopädie Wikipedia und steht unter der
Lizenz Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([01.2] Die technische Zeichnung - Explosionszeichnung)
 Dieser Text basiert auf dem Artikel Explosionszeichnung aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Explosionszeichnung aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([02c-d] Die Normschrift)
 Dieser Text basiert auf dem Artikel Normschrift aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf dem Artikel Normschrift aus der freien Enzyklopädie
Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0 Unported
(Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und
auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([06] Räumliche Ansichten - Die Perspektive)
 Dieser Text basiert auf den Artikeln Perspektive und Darstellende Geometrie aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz
Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Perspektive und Darstellende Geometrie aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz
Creative Commons CC-BY-SA 3.0 Unported (Kurzfassung). Der Text wurde von Andreas Rueff überarbeitet und auf der
Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Infotext ([07] - Die Zentralperspektive (auch Zentralprojektion))
 Dieser Text basiert auf den Artikeln Zentralprojektion , Parallelprojektion und Axonometrie aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Dieser Text basiert auf den Artikeln Zentralprojektion , Parallelprojektion und Axonometrie aus der freien
Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons CC-BY-SA 3.0
Unported (Kurzfassung). Der Text wurde von Andreas Rueff
überarbeitet und auf der Grundlage didaktischer Überlegungen angepasst und gekürzt. In der Wikipedia ist eine Liste der Autoren verfügbar.
Verwendung von LearningApps
Auf dieser Seite sind teilweise auch Online-Übungen verschiedener Ersteller von der Online-Plattform "LearningApps.org" eingebungen. LearningApps.org ist eine nichtkommerzielle Plattform zur Unterstützung von Lehr- und Lernprozessen und wird durch den Nonprofit-Verein LearningApps interaktive Bausteine entwickelt und gepflegt. Die Verwendung von LearningApps.org und jegliche Inhalte, die mit Hilfe unserer Autorenwerkzeuge erstellt wurden, sind für Bildungszwecke kostenlos. Weitere Informationen sind zu finden unter: https://learningapps.org/rechtliches.php
Quellenangaben zu dem Hintergrundbildern:
Die Bilder entstammen aus Pixabay und wurden bearbeitet von A. Rueff.
Bild-1 von Anja Heidsiek auf Pixabay
Bild-2 von Christian Reil auf Pixabay